题目内容
如图所示，竖直放置在水平面上的轻质弹簧上放着质量为1kg的物体A，处于静止状态，若将一个质量为2kg的物体B竖直向下轻放在A上的一瞬间，则B对A的压力大小为（取g=10m/s2）（ ）
| A．20N | B．0 | C．
| D．15N |
放B物体前，A物体受重力和弹簧的支持力，二力平衡，故弹簧弹力F1=mAg=10N；
放上B物体后，先对A、B整体受力分析，受到重力和弹簧的弹力，然后根据牛顿第二定律，有：
（mA+mB）g-F1=（mA+mB）a
解得：
a=g-
=
m/s2
再对B受力分析，受到重力和A对B的支持力，根据牛顿第二定律，有：
mBg-FAB=mBa
解得：
FAB=mB（g-a）=
N
故选C．
放上B物体后，先对A、B整体受力分析，受到重力和弹簧的弹力，然后根据牛顿第二定律，有：
（mA+mB）g-F1=（mA+mB）a
解得：
a=g-
| F1 |
| mA+mB |
| 20 |
| 3 |
再对B受力分析，受到重力和A对B的支持力，根据牛顿第二定律，有：
mBg-FAB=mBa
解得：
FAB=mB（g-a）=
| 20 |
| 3 |
故选C．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
（2009?安徽模拟）如图所示，竖直放置在水平面上的轻质弹簧上叠放着两物块A、B，两者的质量均为2kg，它们处于静止状态．若突然将一个大小为10N、方向竖直向下的力施加在物体A上，则此瞬间A对B的压力大小为：（g=10m/s2）（ ）
（2005?南汇区二模）如图所示，竖直放置在光滑绝缘环上套有一带正电的小球，匀强电场场强方向水平向右，小球绕O点做圆周运动，那么（ ）
如图所示，竖直放置在水平面上的轻质弹簧上放着质量为1kg的物体A，处于静止状态，若将一个质量为2kg的物体B竖直向下轻放在A上的一瞬间，则B对A的压力大小为（取g=10m/s2）（ ）
（2010?南昌一模）如图所示，竖直放置在水平面上的轻弹簧上放着质量为2kg的物体A，处于静止状态．若将一个质量为3kg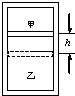
如图所示气缸竖直放置在水平地面上，质量为m的活塞将其缸筒分成甲、乙两气室，两气室中均充有气体．气缸和活塞都是不导热的材料，且不漏气，原先活塞被销钉固定，现拔掉销钉，活塞最终静止在原位置下方距离h处（虚线位置），设活塞移动前后乙气体内能的变化量为△E，不计气体重心改变的影响，则下列说法中正确的是（ ）