题目内容
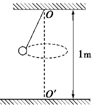如图所示，质量是1kg的小球用长为0.5m的细线悬挂在O点，O点距地面高度为1m，如果使小球绕OO′轴在水平面内做圆周运动，若细线最大承受拉力为12.5N，求：（1）当小球的角速度为多大时，线将断裂．
（2）断裂后小球落地点与悬点的水平距离．（g=10m/s2）
分析：（1）小球靠拉力和重力的合力提供向心力，根据几何关系求出最大向心力，根据向心力公式求出最大角速度；
（2）绳断裂后，小球做平抛运动，根据平抛运动的基本公式即可求解．
（2）绳断裂后，小球做平抛运动，根据平抛运动的基本公式即可求解．
解答：解：（1）小球在水平面内做圆周运动时，由重力G和拉力F的合力提供向心力，当绳子拉力为12.5N时，向心力最大，则有：F合=
=7.5N
根据几何关系得：r=L?
=0.3m
根据向心力公式得：
F合=mω2L?
解得：ω=5rad/s
（2）绳断裂后，小球做平抛运动，初速度v=ωr=1.5m/s
竖直方向下落的高度h=1-0.5×
=0.6m
所以t=
=
s=
s
水平位移为x0=vt=
m
则x=
=0.6m
答：（1）当小球的角速度为5rad/s时，线将断裂．
（2）断裂后小球落地点与悬点的水平距离为0.6m．
| F2-(mg)2 |
根据几何关系得：r=L?
| 3 |
| 5 |
根据向心力公式得：
F合=mω2L?
| 3 |
| 5 |
解得：ω=5rad/s
（2）绳断裂后，小球做平抛运动，初速度v=ωr=1.5m/s
竖直方向下落的高度h=1-0.5×
| 4 |
| 5 |
所以t=
|
| 0.12 |
| ||
| 5 |
水平位移为x0=vt=
3
| ||
| 10 |
则x=
|
答：（1）当小球的角速度为5rad/s时，线将断裂．
（2）断裂后小球落地点与悬点的水平距离为0.6m．
点评：解决本题的关键搞清小球做圆周运动向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
相关题目
（1）下列说法正确的是：
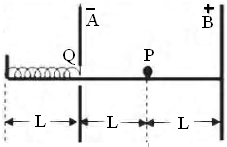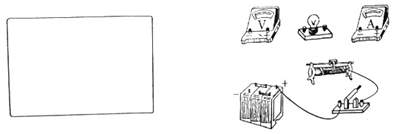
如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的正、负电荷，在两板间形电场强度大小为E匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔中有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为q（q＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．一自然长度为L的轻弹簧左端固定在距A板左侧L处挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小球，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经过一段时间第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的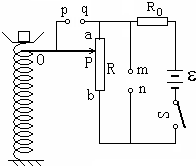
在科技活动中某同学利用自制的电子秤来称量物体的重力，如图所示，为电子秤的原理图．托盘和弹簧的质量均不计，滑动变阻器的滑动端与弹簧上端连接，当托盘中没有放物体时，电压表示数为零；当托盘中的物体的质量改变时，电压表示数发生改变，从而测出物体的质量．设变阻器的总电阻为R，总长度为l，电源电动势为E，内阻为0，弹簧劲度系数为k，弹簧产生的弹力与弹簧压缩量x成正比，即F=k?x．不计一切摩擦和其他阻力，电压表为理想表．
（2009?宜昌模拟）（1）如图所示，在用“自由落体验证机械能守恒定律”的实验中，下面列举了该实验的几个操作步骤，你认为没有必要进行的或者操作不恰当的步骤是
①设小球A质量为mA，小球B质量为mB，为保证实验成功，必须满足mA mB。（选填“大于”、“等于”或“小于”）