��Ŀ����
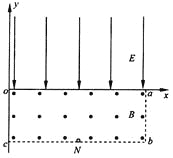
����Ŀ������ͼ��ʾ��ֱ������ϵ![]() �У���������
�У���������![]() ���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB=5.0��10-2T����һ����������
���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB=5.0��10-2T����һ����������![]() �������ǿ�糡���糡ǿ�ȴ�СΪ
�������ǿ�糡���糡ǿ�ȴ�СΪ![]() N/C����֪��������
N/C����֪��������![]() �߳�Ϊ0.06m��ab�߳�Ϊ0.20m����
�߳�Ϊ0.06m��ab�߳�Ϊ0.20m����![]() ���е�
���е�![]() ����һ����Դ��ijʱ�̣�����Դ��ֽ����ų��и�������ȵط�������ʾ�Ϊ
����һ����Դ��ijʱ�̣�����Դ��ֽ����ų��и�������ȵط�������ʾ�Ϊ![]() m/s��ij�ִ��������ӣ�������������
m/s��ij�ִ��������ӣ�������������![]() kg�������
kg�������![]() kg������������������(������������λ��Ч����)
kg������������������(������������λ��Ч����)
(1)�����ڴų����˶��İ뾶��
(2)��![]() ��������������У��ڴų����˶������·��Ϊ����?
��������������У��ڴų����˶������·��Ϊ����?
(3)����Դ��-![]() ������������ӣ����������
������������ӣ����������![]() ���뿪���õ�ʱ�䡣
���뿪���õ�ʱ�䡣
���𰸡���1��0.02m (2)0.21m (3)![]()
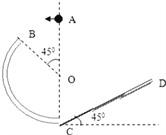
�������������������1�������˶��Ĺ켣��ͼ����ţ�ٵڶ����ɿɵã�

![]()
���:![]() m��
m��
��2������ѧ֪ʶ��֪������Ҷ�Ӧ��̵Ļ�������ͼ��֪��![]() =60��
=60��
��̵Ļ��������·��![]() m=0.21m��
m=0.21m��
��3�������ڴų��е�����![]()
�����ڴų�����![]() �˶���ʱ��
�˶���ʱ��![]()
�����ڵ糡�еļ��ٶ�![]()
![]()
��ã�![]()
��ɽ�������ڵ糡�������˶���ʱ��Ϊt2+t3=2t=2.0��10��7s
��ͼ��֪![]() ,��
,��![]()
�����ڴų����˶��ĵڶ�����ʱ��![]()
�����˶�����ʱ��![]() ��
��

��ϰ��ϵ�д�
 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
�����Ŀ