题目内容
如图所示,一根长度为l的轻杆两端各固定一个可视为质点的小球A和B.两球质量均为m,轻杆可绕其中点在竖直平面内匀速转动.
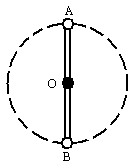
(1)若直杆转动周期T=2π![]() .求直杆转到图示位置时,A,B两球对杆作用力各是多少,方向如何.
.求直杆转到图示位置时,A,B两球对杆作用力各是多少,方向如何.
(2)若直杆转到图示位置时,杆对A球的拉力恰好等于球的重力.求此时杆的转动周期及B球对杆的作用力.
答案:
解析:
解析:
|
(1)若周期T=2π
ω= 小球运动需要的向心力大小为
F向=mω2R=m 对A球:最高点,小球受的重力大于其需要的向心力,故向下压杆.即杆对球有向上的支持力
mg- ∴
故A对杆向下压力大小
FN= 对B球:杆对球的拉力FN与重力的合力提供小球运动的向心力.
FN-mg=mω2R,∴FN=mg+mω2R= 故球对杆向下的拉力大小为 (2)当转到图示位置时;杆对球A产生向下的大小为mg的拉力,则
即
2mg=m 故直杆的转动周期
Tx= B球在最低点有F-mg=m 故球对直杆竖直向下的拉力等于3mg. |

练习册系列答案
相关题目
 如图所示,一根长直导线穿过载有恒定电流的金属圆环的中心且垂直于环平面,导线和环中的电流方向如图.则环受到的磁场力为( )
如图所示,一根长直导线穿过载有恒定电流的金属圆环的中心且垂直于环平面,导线和环中的电流方向如图.则环受到的磁场力为( )| A、沿环半径向外 | B、环半径向内 | C、水平向左 | D、等于零 |
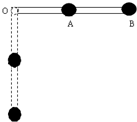 如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )
如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )A、B球的速率为
| ||||
B、B球的机械能减少了
| ||||
C、A球的机械能减少了
| ||||
| D、每个小球的机械能都不变 |
 如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )
如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )A、小球过最低点时的速度大小为
| ||
B、小球过最高点时的速度大小为
| ||
| C、小球过最低点时受到杆的拉力大小为5mg | ||
| D、小球过最高点时受到杆的支持力为零 |
 如图所示,一根长为l,质量为m的匀质软绳悬于O点,若将其下端向上提起使其对折,则做功至少为( )
如图所示,一根长为l,质量为m的匀质软绳悬于O点,若将其下端向上提起使其对折,则做功至少为( )| A、mgl | ||
B、
| ||
C、
| ||
D、
|
 如图所示,一根长为l1的橡皮条和一根长为l2的绳子(l1<l2)悬于同一点,橡皮条的另一端系一A球,绳子的另一端系一B球,两球质量相等,现从悬线水平位置(绳拉直,橡皮条保持原长)将两球由静止释放,当两球摆至最低点时,橡皮条的长度与绳子长度相等,此时两球速度的大小为( )
如图所示,一根长为l1的橡皮条和一根长为l2的绳子(l1<l2)悬于同一点,橡皮条的另一端系一A球,绳子的另一端系一B球,两球质量相等,现从悬线水平位置(绳拉直,橡皮条保持原长)将两球由静止释放,当两球摆至最低点时,橡皮条的长度与绳子长度相等,此时两球速度的大小为( )