题目内容
如图所示，在一个半径为R、质量为M的均匀球体中，紧贴球的边缘挖去一个半径为R/2的球形空穴后，剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大？
答案：
解析：
提示：
解析：
答案：
解析：把整个球体对质点的引力F看成是挖去的小球体对质点的引力F1和剩余部分对质点的引力F2之和，即F＝F1＋F2
填补上空穴的完整球体对质点m的引力为
F＝
挖去的半径为R/2的小球体的质量为
，则
＝ρ×
M
F1＝
挖去球穴后的剩余部分对球外质点m的引力
F2＝F－F1＝
．
思路分析：挖去空穴后剩余部分已不再是质量均匀分布的球体，无法求r，不能直接应用万有引力公式计算引力．如果将挖去的部分填补上成为匀质球后，由万有引力公式可求解，再据力的合成与分解求剩余部分对m的引力．
提示：
物体不能看作质点时，不能应用万有引力公式求解，想办法建立理想模型后再应用公式求解．万有引力遵循力的合成与分解原则．
练习册系列答案
相关题目
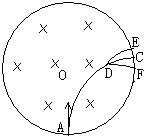（2004?惠州一模）如图所示，在一个半径为R的圆形区域内存在着匀强磁场，磁场方向垂直于圆面向里，一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内，粒子将做圆周运动到达磁场边界的C点，但在粒子经过D点时，恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子，关于这个新粒子的运动情况，以下判断正确的是（ ）
如图所示，在一个半径为R的圆形区域内存在着匀强磁场，磁场方向垂直于圆面向里．一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内，粒子将做圆周运动到达磁场边界的C点，但在粒子经过D点时，恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子，关于这个新粒子的运动情况，以下判断正确的是（ ）
