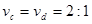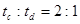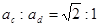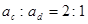题目内容
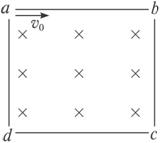
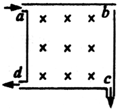如图所示，正方形容器处在匀强磁场中，一束电子从a孔沿a→b方向垂直射入容器内的匀强磁场中，结果一部分电子从小孔c射出，一部分电子从小孔d射出，则从c、d两孔射出的电子（ ）分析：带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，有Bqv=m
，得出半径公式r=
，根据半径关系得出粒子的速度关系．再根据an=
，可确定运动的加速度之比．
带电粒子运行的周期T=
，根据圆心角求出运行时间t=
T．从而求出运动时间之比．
| v2 |
| r |
| mv |
| Bq |
| v2 |
| r |
带电粒子运行的周期T=
| 2πm |
| Bq |
| θ |
| 2π |
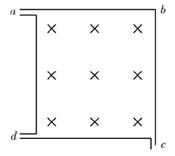
解答：解：设磁场边长为a，如图所示，粒子从c点离开，其半径为rc，粒子从d点离开，其半径为rd；
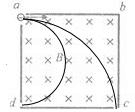
由Bqv=m
，得出半径公式r=
，
又由运动轨迹知 rc=2rd 则vc：vd=2：1；
由T=
，根据圆心角求出运行时间t=
T．
运行时间 td=
，tc=
．则tc：td=1：2．
根据an=
，可得ac：ad=2：1；
故选：ABD
由Bqv=m
| v2 |
| r |
| mv |
| Bq |
又由运动轨迹知 rc=2rd 则vc：vd=2：1；
由T=
| 2πm |
| Bq |
| θ |
| 2π |
运行时间 td=
| T |
| 2 |
| T |
| 4 |
根据an=
| v2 |
| r |
故选：ABD
点评：本题属于带电粒子在磁场中的偏转中典型题目，此类题的关键在于确定圆心及由几何关系求出半径．掌握带电粒子在匀强磁场中做匀速圆周运动的半径公式r=
，和周期公式T=
．
| mv |
| Bq |
| 2πm |
| Bq |
练习册系列答案
备战中考寒假系列答案
相关题目
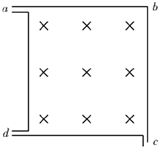如图所示，正方形容器处在匀强磁场中，一束电子从a孔垂直进入磁场射入容器中，其中一部分从c孔射出，一部分从d孔射出，则下列说法正确的是（ ）
∶1
