题目内容
在用高级沥青铺设的高速公路上，汽车的设计时速是108km/h.汽车在这种路面上行驶时，它的轮胎与地面的最大静摩擦力等于车重的0.6 (取g＝10m/s2) .求:
(1)如果汽车在这种高速路的水平弯道上拐弯，假设弯道的路面是水平的，拐弯时不产生横向滑动，其弯道的最小半径是多少？
(2)如果高速路上设计了圆弧形拱桥做立交桥，要使汽车能够不离开地面安全通过圆弧拱桥，这个圆弧拱桥的半径应满足什么条件？
（1）Rmin=150m（2）R≥90m
解析试题分析：（1）转弯时，摩擦力提供向心力：0.6mg=m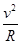
,代入数值解得：Rmin=150m （6分）
(2)要安全过圆拱桥，肯定是刚好过最高点，那么就是重力提供向心力:
mg=m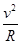，代入数值解得：Rmin=90m （6分）
所以，R≥90m
考点：牛顿第二定律；向心力．
点评：解决本题的关键知道汽车在水平路面上拐弯靠静摩擦力提供向心力，在拱桥的顶端，靠重力和支持力的合力提供向心力，当支持力为零时，仅靠重力提供向心力．
练习册系列答案
相关题目