题目内容
（12分）当物体从高空下落时，所受阻力会随物体的速度增大而增大，因此经过下落一段距离后将匀速下落，这个速度称为此物体下落的收尾速度。研究发现，在相同环境条件下，球形物体的收尾速度仅与球的半径和质量有关．下表是某次研究的实验数据
|
小球编号 |
A |
B |
C |
D |
E |
|
小球的半径（×10－3m） |
0.5 |
0.5 |
1.5 |
2 |
2.5 |
|
小球的质量（×10－6kg） |
2 |
5 |
45 |
40 |
100 |
|
小球的收尾速度（m/s） |
16 |
40 |
40 |
20 |
32 |
（1）根据表中的数据，求出B球与C球在达到终极速度时所受阻力之比．
（2）根据表中的数据，归纳出球型物体所受阻力f与球的速度大小及球的半径的关系（写出有关表达式、并求出比例系数）．
（3）现将C号和D号小球用轻质细线连接，若它们在下落时所受阻力与单独下落时的规律相同．让它们同时从足够高的同一高度下落，试求出它们的收尾速度；并判断它们落地的顺序．
（1）1：9（2）k＝4.9Ns/m3（3）C球先落地
【解析】（1）球在达到终极速度时为平衡状态，有
f ＝mg（2分）
则fB：fC ＝mB ：mC
带入数据得fB：fC＝1：9（4分）
（2）由表中A、B球的有关数据可得，阻力与速度成正比；即
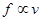（5分）
由表中B、C球有关数据可得，阻力与球的半径的平方成正比，即
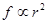
得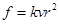
（6分）
k＝4.9Ns/m3 （8分） （或k＝5Ns/m3）
（3）将C号和D号小球用细线连接后，其收尾速度应满足
mCg＋mDg＝fC ＋fD
即mCg＋mDg＝kv(rC2＋rD2)
代入数据得v＝27.2m/s（10分）
比较C号和D号小球的质量和半径，可判断C球先落地．（12分）
本题考查力与运动的关系，当球速度最大时受力平衡，由阻力与重力的关系可知B、C两点的阻力之比，由表中A、B球的有关数据可得，阻力与速度成正比，由表中B、C球有关数据可得，阻力与球的半径的平方成正比，可大概写出利于速度和半径的关系，求得常数k即可
开心蛙状元测试卷系列答案