题目内容
从地面上以初速度vo=10m/s竖直向上抛出一质量为m=0.2kg的小球，若运动过程中小球受到的空气阻力与其速率成正比关系，球运动的速率随时间变化规律如图所示，t1时刻到达最高点，再落回地面，落地时速率为v1=2m/s，且落地前球已经做匀速运动。（g=10m/s2）求：
（1）球从抛出到落地过程中克服空气阻力所做的功；
（2）球抛出瞬间的加速度大小；
【答案】
（1）9.6J（2）60m/s2
【解析】（1）由动能定理得Wf＝
mv12－mv02（2分）
克服空气阻力做功W＝－Wf＝mv02－mv12 ＝9.6J（2分）
（2）空气阻力f＝kv（1分）
落地前匀速运动，则mg－kv1＝0（2分）
刚抛出时加速度大小为a 0，则
mg＋kv0＝m a0（2分）
解得a0＝（1＋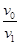
）g＝60m/s2（1分）
本题考查动能定理的应用，先选取研究过程，在从抛出到落地过程中重力做功为零，只有阻力做功，所以阻力做功等于动能的减小量，当阻力等于重力时，物体下落速度最大，此时加速度为零，可求得常数k与重力关系，当刚抛出时阻力最小，加速度最大，结合速度时间图像列出牛顿第二定律的公式，联立即可
练习册系列答案
相关题目
