��Ŀ����
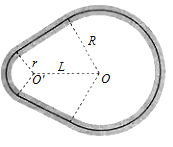
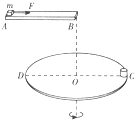
����Ŀ����ͼ��ʾ��ˮƽ���õ�Բ�̰뾶Ϊ![]() �������Ե
�������Ե![]() ��̶�һ���߶Ȳ��Ƶ�СͰ����Բ��ֱ��
��̶�һ���߶Ȳ��Ƶ�СͰ����Բ��ֱ��![]() �����Ϸ�����һ��ˮƽ����
�����Ϸ�����һ��ˮƽ����![]() ��������
��������![]() ƽ�У������Ҷ�
ƽ�У������Ҷ�![]() ��Բ��Բ��
��Բ��Բ��![]() ��ͬһ��ֱ���ϣ���߶Ȳ�Ϊ
��ͬһ��ֱ���ϣ���߶Ȳ�Ϊ![]() ���ڻ�����˾�ֹ��������Ϊ
���ڻ�����˾�ֹ��������Ϊ![]() ����飨����Ϊ�ʵ㣩�������뻬����Ķ�Ħ������Ϊ
����飨����Ϊ�ʵ㣩�������뻬����Ķ�Ħ������Ϊ![]() ������һ��СΪ
������һ��СΪ![]() ��ˮƽ����������������ͬʱ��Բ�̴�ͼʾλ���Խ��ٶ�
��ˮƽ����������������ͬʱ��Բ�̴�ͼʾλ���Խ��ٶ�![]() ���ƴ���Բ��
���ƴ���Բ��![]() ����ֱ������ת������������һ��ʱ���������ڻ����ϼ������У���
����ֱ������ת������������һ��ʱ���������ڻ����ϼ������У���![]() ��ˮƽ�׳���ǡ������СͰ�ڣ��������ٶ�ȡ
��ˮƽ�׳���ǡ������СͰ�ڣ��������ٶ�ȡ![]() ��
��
��1������뿪![]() ��ˮƽ�׳��ij��ٶ�
��ˮƽ�׳��ij��ٶ�![]() ��
��
��2����������������ʱ��ͻ����ij��ȣ������ǡ������СͰ�ڣ����������õ����ʱ�䣮
���𰸡�(1) ![]() (2)
(2) ![]()
����������������������B���뿪����ƽ���˶�������ƽ���˶��Ĺ��ɿ����B����ٶȣ���Բ��תһȦ�����ǡ�õ���СͰ����ʱ������ʱ����̣�Բ��תһȦ��ʱ�����ȼ����˶����ȼ����˶���ƽ���˶�����ʱ��֮�������
��1�����ƽ���˶�������ֱ�����У� ![]()
��ã� ![]()
����뿪����ʱ���ٶȣ� ![]()
��2���������ʱ�ļ��ٶ�Ϊ![]() ����ţ�ٵڶ����ɣ�
����ţ�ٵڶ����ɣ� ![]()
�������ݵã� ![]()
��ȥ��������ţ�ٵڶ����ɵã� ![]() ��
��
�������ݵã� ![]()
��ת��һȦʱ���룬����ʱ����̣���ת��һȦʱ��Ϊ�� ![]()
����ڻ������ȼ��ٺ���٣��У� ![]()
��黬��ʱ�䡢�׳��ڿ���ʱ����Բ�����ڹ�ϵ�� ![]()
������ʽ�ã� ![]() ��
��