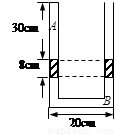题目内容
如图所示，U形管两细管粗细均匀长度相等，左端封闭，右端开口，水平部分长20cm．有两段8cm长水银柱等高，各封住长为30cm的空气柱A和长为40cm的空气柱B，两气体温度均为27°C，大气压强恒定．现使A、B温度缓慢升高，最终都达到57°C．问：（1）空气柱A的最终长度．
（2）右管内水银柱移动的距离．
【答案】分析：（1）对A气体，假设水银柱未进入水平管，根据气体等压变化列出方程求解
（2）对B气体，等压变化列出方程求解
解答：解：（1）对A气体，假设水银柱未进入水平管，气体等压变化遵循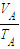
=
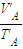
代入数据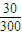
=
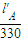
解得l′A=33cm 故假设正确
（2）对B气体，等压变化遵循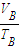
=
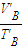
代入数据解得l′B=44cm
右管内水银柱向上移动距离为△h=44-40+3cm=7cm
答：（1）空气柱A的最终长度是33cm．
（2）右管内水银柱移动的距离是7cm．
点评：只要封闭气体的物质的量没有变化即为一定质量的封闭气体，只要能够判定封闭气体的哪一个物理量没有变化，就能确定封闭气体是发生等容变化、等温变化还是等压变化，如果三个物理量都发生变化，那么就利用理想气体状态方程解决．
（2）对B气体，等压变化列出方程求解
解答：解：（1）对A气体，假设水银柱未进入水平管，气体等压变化遵循
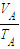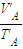
=代入数据
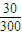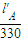
=解得l′A=33cm 故假设正确
（2）对B气体，等压变化遵循
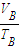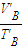
= 代入数据解得l′B=44cm
右管内水银柱向上移动距离为△h=44-40+3cm=7cm
答：（1）空气柱A的最终长度是33cm．
（2）右管内水银柱移动的距离是7cm．
点评：只要封闭气体的物质的量没有变化即为一定质量的封闭气体，只要能够判定封闭气体的哪一个物理量没有变化，就能确定封闭气体是发生等容变化、等温变化还是等压变化，如果三个物理量都发生变化，那么就利用理想气体状态方程解决．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
（2012?长宁区二模）如图所示，U形管两细管粗细均匀长度相等，左端封闭，右端开口，水平部分长20cm．有两段8cm长水银柱等高，各封住长为30cm的空气柱A和长为40cm的空气柱B，两气体温度均为27°C，大气压强恒定．现使A、B温度缓慢升高，最终都达到57°C．问：
