Question

两带电小球，电荷量分别为+q和-q，固定在一长度为l的绝缘细杆的两端，置于电场强度为E的匀强电场中，杆与场强方向平行，其位置如下图所示．若此杆绕过O点垂直于杆的轴线转过，则在此转动过程中电场力做的功为

[　　]

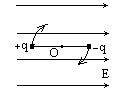
A．零

B．qEl

C．2qEl

D．πqEl

Answer 1

答案：C
解析：

解析　本题要求在电场中移动电荷时，电场力对电荷做功的多少．解决问题的关键是：针对具体问题，选择电场力做功的计算方法．其主要思路有： 　　(1)用电功的定义式W＝Fs计算，中学阶段限于匀强电场中使用； 　　(2)利用结论“电场力做的功等于电荷电势能增量的负值”(或等于电势能的变化)计算，这个方法在已知电荷电势能的值时比较方便； 　　(3)用公式W＝qU计算，在中学阶段，一般不要求带符号运算，而只取q，U的绝对值计算，对于功W的正负，可依据提供的物理模型，或根据题设条件构想物理模型，利用所学知识判定； 　　(4)利用动能定理计算，在知道电荷动能的改变量，以及知道除电场力以外其他力做功数量时，使用动能定理较方便． 　　本题利用上述方法1、方法3均较方便． 　　解法一：因在电场中任意两点移动电荷时，电场力对电荷做的功，与移动电荷的路径无关，可设想两电荷均沿绝缘杆移动到相应位置，则 　　W＝Fl＋Fl＝Eql＋Eql＝2Eql 　　故选项C正确． 　　解法二：由匀强电场中电势差跟电场强度的关系可知，两点电荷所在位置间的电势差 　　U＝El 　　电场力对两电荷均做正功，则 　　W＝qU＋qU＝2qEl，即应选C．