题目内容
（2009?枣庄一模）如图所示，一匀强磁场磁感应强度为B；方向向里，其边界是半径为R的圆，AB为圆的一直径．在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子，粒子重力不计．（1）有一带电粒子以v=
| 2qBR | m |
（2）若磁场的边界是绝缘弹性边界（粒子与边界碰撞后将以原速率反弹），某粒子沿半径方向射入磁场，经过2次碰撞后回到A点，则该粒子的速度为多大？
（3）若R=3cm、B=0.2T，在A点的粒子源向圆平面内的各个方向发射速度均为3×105m/s、比荷为108C/kg的粒子．试用阴影图画出粒子在磁场中能到达的区域，并求出该区域的面积（结果保留2位有效数字）．
分析：（1）根据洛伦兹力提供向心力，求出粒子的半径，通过几何关系得出圆弧所对应的圆心角，根据周期公式，结合t=
T求出粒子在磁场中运动的时间．
（2）粒子径向射入磁场，必定径向反弹，作出粒子的轨迹图，通过几何关系求出粒子的半径，从而通过半径公式求出粒子的速度．
（3）根据粒子的半径公式求出粒子的轨道半径，作出粒子轨迹所能到达的部分，根据几何关系求出面积．
| α |
| 2π |
（2）粒子径向射入磁场，必定径向反弹，作出粒子的轨迹图，通过几何关系求出粒子的半径，从而通过半径公式求出粒子的速度．
（3）根据粒子的半径公式求出粒子的轨道半径，作出粒子轨迹所能到达的部分，根据几何关系求出面积．
解答：解：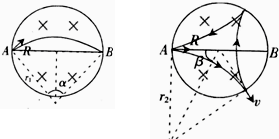
（1）由qvB=m
得r1=2R
粒子的运动轨迹如图所示，则α=
因为周期T=
．
运动时间t=
T=
．
（2）粒子运动情况如图所示，β=
．
r2=Rtanβ=
R
由qvB=m
得v=
（3）粒子的轨道半径r3=
=1.5cm
粒子到达的区域为图中的阴影部分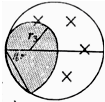
区域面积为S=
πr32+2×
π(2r3)2-
r32=9.0×10-4m2
答：（1）此粒子在磁场中运动的时间为
．
（2）该粒子的速度为v=
．
（3）该区域的面积为9.0×10-4m2．
（1）由qvB=m| v2 |
| r1 |
粒子的运动轨迹如图所示，则α=
| π |
| 3 |
因为周期T=
| 2πm |
| qB |
运动时间t=
| α |
| 2π |
| πm |
| 3qB |
（2）粒子运动情况如图所示，β=
| π |
| 3 |
r2=Rtanβ=
| 3 |
由qvB=m
| v2 |
| r2 |
| ||
| m |
（3）粒子的轨道半径r3=
| mv |
| Bq |
粒子到达的区域为图中的阴影部分
区域面积为S=
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
答：（1）此粒子在磁场中运动的时间为
| πm |
| 3qB |
（2）该粒子的速度为v=
| ||
| m |
（3）该区域的面积为9.0×10-4m2．
点评：本题考查了带电粒子在磁场中的运动问题，需掌握粒子的半径公式和周期公式．该题对数学几何能力要求较高，需加强这方面的训练．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
（2009?枣庄一模）如图所示是给墙壁粉刷涂料用的“涂料滚”的示意图．使用时，用撑竿推着粘有涂料的涂料滚沿墙壁上下缓缓滚动，把涂料均匀地粉刷到墙上．撑竿的重力和墙壁的摩擦均不计，且撑竿足够长，粉刷工人站在离墙壁一定距离处缓缓上推涂料滚，设该过程中撑竿对涂料滚的推力为F1，涂料滚对墙壁的压力为F2，则（ ）
（2009?枣庄一模）如图所示，平行金属导轨与水平面间的倾角为θ，导轨电阻不计，与阻值为R的定值电阻相连．匀强磁场垂直穿过导轨平面，磁感应强度为B．有一质量为m、长为l的导体棒从ab位置以平行于斜面的大小为v的初速度向上运动，最远到达a′b′的位置．已知ab与a′b′之间的距离为s；导体棒电阻的阻值也为R，与导轨之间的动摩擦因数为μ．则（ ）
（2009?枣庄一模）听说水果也能做电池，某兴趣小组的同学用一个柠檬做成电池．他们猜想水果电池内阻可能较大，从而设计了一个如图所示电路来测定该柠檬电池的电动势和内电阻．实验中他们多次改变电阻箱的电阻值，记录下电阻箱的阻值及相应的电流计示数，并算出电流的倒数，将数据填在如下的表格中．
（2009?枣庄一模）某交流发电机给灯泡供电，产生正弦式交变电流的图象如图所示，下列说法中正确的是（ ）