题目内容
一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应之间△t的比值定义为角加速度β（即β=| △ω | △t |
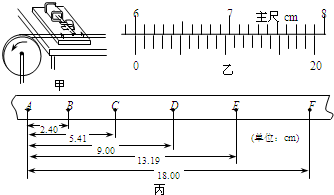
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，停止转动和打点，取下纸带，进行测量．
（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为
6.000
6.000
cm；（2）由图丙可知，打下计数点D时，圆盘转动的角速度为
6.5
6.5
rad/s；（3）纸带运动的加速度大小为
0.60
0.60
m/s2，圆盘转动的角加速度大小为10
10
rad/s2．▲请注意：本题（2）、（3）问中的结果均要求保留2位有效数字．
分析：（1）游标卡尺的读数等于主尺读数加上游标读数，不需估读．
（2）根据某段时间内的平均速度等于中间时刻的瞬时速度求出D点的线速度，结合v=rω求出圆盘的角速度．
（3）根据相等时间内的位移之差是一恒量求出纸带运动的加速度，结合加速度与角加速度的关系求出圆盘角加速度的大小．
（2）根据某段时间内的平均速度等于中间时刻的瞬时速度求出D点的线速度，结合v=rω求出圆盘的角速度．
（3）根据相等时间内的位移之差是一恒量求出纸带运动的加速度，结合加速度与角加速度的关系求出圆盘角加速度的大小．
解答：解：（1）因为游标的零刻度线对准主尺上的6，知主尺读数为60mm，游标卡尺的精确度为0.05，第零根与主尺刻度线对齐，则游标卡尺的读数为：60mm+0.05×0=60.00mm=6.000cm．
（2）D点的瞬时速度vD=
=
m/s=0.389m/s．
则圆盘的角速度ω=
=
≈6.5rad/s．
（3）xAB=2.40cm，xBC=3.01cm，xCD=3.59cm，xDE=4.19cm，
则a1=
，a2=
则a=
=
≈0.60m/s2．因为a=
=
=rβ，则角加速度β=
=
=10rad/s2．
故答案为：（1）6.000，（2）6.5，（3）0.59-0.60，9.8-10．
（2）D点的瞬时速度vD=
| xCE |
| 2T |
| (13.19-5.41)×10-2 |
| 0.2 |
则圆盘的角速度ω=
| vD |
| r |
| 0.389 |
| 0.06 |
（3）xAB=2.40cm，xBC=3.01cm，xCD=3.59cm，xDE=4.19cm，
则a1=
| xCD-xAB |
| 2T2 |
| xDE-xBC |
| 2T2 |
则a=
| a1+a2 |
| 2 |
| xCD+xDE-xAB-xBC |
| 4T2 |
| △v |
| △t |
| r△ω |
| △t |
| a |
| r |
| 0.6 |
| 0.06 |
故答案为：（1）6.000，（2）6.5，（3）0.59-0.60，9.8-10．
点评：解决的关键掌握游标卡尺的读数方法，会通过纸带求解瞬时速度和加速度，以及知道加速度与角加速度的关系．
练习册系列答案
相关题目
一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量△ω与对应时间△t的比值定义为角加速度β．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D…为计数点，相邻两计数点间有四个点未画出）
一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动．用下面的方法测量它匀速转动时的角速度．
一个有一定厚度的圆盘A，可以绕通过中心垂直于盘面的水平轴转动．用下面的方法测量它匀速转动的角速度．