题目内容

（13分）在一广阔的匀强磁场中，建立一直角坐标系，如图所示，在坐标系的原点O释放一速率为v，质量为m电荷量为十q的粒子（重力不计），释放时速度方向垂直于B的方向，且与x轴成30°角，

则(1)其第一次经过y轴时，轨迹与y轴交点离O点距离为多少？（不考虑空气阻力）
（2粒子从O点开始运动到穿过y轴时所用的时间
（3粒子做圆周运动圆心的坐标

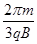(1)  (2)  (3) 圆心坐标为（）

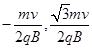解析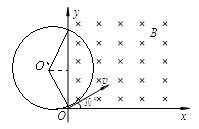
试题分析：（1）由题意画出带电粒子的运动轨迹，洛伦兹力充当向心力由牛顿第二定律得qBv=   ①
设带电粒子轨迹的轨道半径为R，纵坐标为y，由几何关系 sin600 =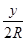   ②
由①②式解得y=   
(2）由匀速圆周运动的周期公式T=    ③
所以带电粒子的运动时间t=   ④
由①、③、④式求得t=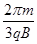
(3)设粒子做圆周运动的圆心坐标位（x，y）
由cos60°=  得 x=
圆心坐标为（）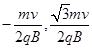
考点：洛伦兹力 左手定则 牛顿第二定律

练习册系列答案
相关题目

如图所示，在光滑绝缘的水平面内，对角线AC将边长为L的正方形分成ABC和ADC两个区域，ABC区域有垂直于水平面的匀强磁场，ADC区域有平行于DC并由C指向D的匀强电场．质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域，从对角线AC的中点O进入电场区域．

（1）判断磁场的方向并求出磁感应强度B的大小．
（2）讨论电场强度E在不同取值时，带电粒子在电场中运动的时间t．

如图，虚线的左下方存在匀强磁场大小B。A、B是完全相同的两个质量均为m的小金属球(可看做质点)。A带正电q,B不带电且用长为L的细绳竖直悬挂在O点。整个空间存在竖直向上的匀强电场，场强大小为，A球在M点沿竖直向下射入磁场B，到达N点时速度水平，在N点与B球碰后交换速度，碰后B球刚好能以L为半径，在竖直平面内运动到圆周最高点，A球则水平匀速从Q点射出。(重力加速度为g)不计一切摩擦。已知AB与水平面夹角为45°，BC与水平面夹角为θ=30°。

求：(1)B球被碰后的速度大小。
(2)A球射入点M到N的距离。
(3)A球从Q点水平射出时距N点的距离。（笔者感觉原试卷缺少条件，故做了改编，仅供参考）

（14分）如图所示，在正方形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场。在t=0时刻，一位于正方形区域中心O的粒子在abcd平面内向各个方向发射出大量带正电的粒子，所有粒子的初速度大小均相同，粒子在磁场中做圆周运动的半径恰好等于正方形边长，不计重力和粒子之间的相互作用力。已知平行于ad方向发射的粒子在t=t0时刻刚好从磁场边界cd上的某点离开磁场，（已知）求：

（1）粒子的比荷；
（2）从粒子发射到粒子全部离开磁场所用的时间；
（3）假设粒子发射的粒子在各个方向均匀分布，在t=t0时刻仍在磁场中的粒子数与粒子发射的总粒子数之比。

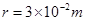（8分）在真空中，半径的圆形区域内有匀强磁场，方向如图所示，磁感应强度B="0.2" T，一个带正电的粒子以初速度从磁场边界上直径ab的一端a射入磁场，已知该粒子的比荷，不计粒子重力．

（1）求粒子在磁场中做匀速圆周运动的半径；
（2）若要使粒子飞离磁场时有最大偏转角，求入射时与ab的夹角及粒子的最大偏转角．

如图所示，在x轴的上方（y＞0的空间内）存在着垂直于纸面向里、磁感应强度为B的匀强磁场，一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角，若粒子的质量为m，电量为q，求：

（1）该粒子在磁场中作圆周运动的轨道半径；
（2）粒子在磁场中运动的时间。

如图所示，宽x=2cm的有界匀强磁场的纵向范围足够大，磁感应强度的方向垂直纸面向内，大小为0.01T。现有一群比荷q/m=4×107C/kg的正粒子，从O点以相同的速率2×104m/s沿纸面不同方向进入磁场，粒子重量忽略不计（）。求：

（1）粒子在磁场中做圆周运动的半径；
（2）所有打在y轴上的粒子在磁场中运动的最长时间；
（3）打在分界线x=2cm上粒子的分布范围.

（10分）在相互垂直的匀强电场和匀强磁场中，有一倾角为θ，足够长的光滑绝缘斜面，磁感应强度为B，方向垂直纸面向外，电场方向竖直向上。有一质量为m，带电荷量为+q的小球静止在斜面顶端，这时小球对斜面的正压力恰好为零，如图所示，若迅速把电场方向反转成竖直向下。

求：（1）小球能在斜面上连续滑行多远？
（2）所用时间是多少？

如图所示，一个矩形金属线框与条形磁铁的中轴线OO′在同一平面 内．下列不能产生感应电流的操作是

A．使线框以OO′为轴转动
B．使线框以边为轴转动
C．使线框以边为轴转动
D．使线框向右加速平移

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网