题目内容
 (2010?肇庆一模)如下图所示,真空室内存在宽度为s=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直纸面向里.紧挨边界ab的中央有一点状α粒子放射源S,可沿纸面向各个方向放射速率相同的α粒子,它的速率v=3.2×106m/s.磁场边界ab、cd足够长,cd为厚度不计的金箔,金箔右侧cd与MN之间有一宽度为L=12.0cm的无场区,MN右侧为固定在O点的带电量为Q=-2.0×10-6C的点电荷形成的电场区域(点电荷左侧的电场分布以MN为界限).不计α粒子的重力,α粒子的质量和带电量分别是m=6.64×10-27kg、Q=3.2×10-19C,静电力常量k=9.0×109N?m2/C2,sin37°=0.6,cos37°=0.8.
(2010?肇庆一模)如下图所示,真空室内存在宽度为s=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直纸面向里.紧挨边界ab的中央有一点状α粒子放射源S,可沿纸面向各个方向放射速率相同的α粒子,它的速率v=3.2×106m/s.磁场边界ab、cd足够长,cd为厚度不计的金箔,金箔右侧cd与MN之间有一宽度为L=12.0cm的无场区,MN右侧为固定在O点的带电量为Q=-2.0×10-6C的点电荷形成的电场区域(点电荷左侧的电场分布以MN为界限).不计α粒子的重力,α粒子的质量和带电量分别是m=6.64×10-27kg、Q=3.2×10-19C,静电力常量k=9.0×109N?m2/C2,sin37°=0.6,cos37°=0.8.(1)金箔cd被α粒子射中区域的长度y值;
(2)打在金箔d端距cd中心最远的粒子沿直线穿出金箔,经过无场区进入电场即开始以O点为圆心做匀速圆周运动,垂直打在放置于中心线上的荧光屏FH上的E点(未画出),计算
. | OE |
(3)计算此α粒子从金箔穿出时损失的动能.
分析:(1)粒子在匀强磁场中做匀速圆周运动,由洛仑兹力提供向心力,由牛顿第二定律求出轨迹半径.当α粒子运动的圆轨迹与cd相切时上端偏离O′最远,当α粒子沿Sb方向射入时,下端偏离O′最远,画出临界的两条轨迹,由几何知识求出金箔cd被α粒子射中区域的长度y值;
(2)打在金箔d端距cd中心最远的粒子沿直线穿出金箔,经过无场区进入电场,开始以O点为圆心做匀速圆周运动,画出轨迹,由几何关系求出
的长度;
(3)此α粒子从金箔穿出后以O点为圆心做匀速圆周运动,库仑力提供向心力,由牛顿纴第二定律求出此粒子的速度,即可得到从金箔穿出时损失的动能.
(2)打在金箔d端距cd中心最远的粒子沿直线穿出金箔,经过无场区进入电场,开始以O点为圆心做匀速圆周运动,画出轨迹,由几何关系求出
. |
| OE |
(3)此α粒子从金箔穿出后以O点为圆心做匀速圆周运动,库仑力提供向心力,由牛顿纴第二定律求出此粒子的速度,即可得到从金箔穿出时损失的动能.
解答:解:(1)粒子在匀强磁场中做匀速圆周运动,由洛仑兹力提供向心力.qvB=m
…①
由①式可得:R=0.2m
如答图所示, 当α粒子运动的圆轨迹与cd相切时上端偏离O′最远,由几何关系可得:O′P=
当α粒子运动的圆轨迹与cd相切时上端偏离O′最远,由几何关系可得:O′P=
…②
将数据代入②式可得:O′P=0.16m
当α粒子沿Sb方向射入时,下端偏离O′最远,由几何关系可得:O′Q=
…③
将数据代入②式可得:O′Q=0.16m
故金箔被α粒子射中区域的长度为:
y=O′P+O′Q=0.31m…④
(2)如图所示,OE为α粒子绕O点做圆周运动的半径r,α粒子在无场区域内做直线运动与MN相交,下偏距离为y′,
因为R=0.2m,L=0.12m,O′Q=0.16m,
所以sinα=
=0.6=sin37°,则:
y′=Ltan37°…⑤
所以圆周运动的半径为:r=
…⑥
将数据代入⑥式可得:r=0.31m…⑦
即|OE|的长度为0.31m.
(3)设α粒子穿出金箔时的速度为v′,由牛顿第二定律可得:k
=m
…⑧
α粒子从金箔穿出时损失的动能为△Ek,则:
△Ek=
mv2-
mv′2…⑨
由⑨式可得:△Ek=2.5×10-14J…⑩
答:
(1)金箔cd被α粒子射中区域的长度y值是0.31m;
(2)
的长度是0.31m;
(3)此α粒子从金箔穿出时损失的动能是2.5×10-14J.
| v2 |
| R |
由①式可得:R=0.2m
如答图所示,
 当α粒子运动的圆轨迹与cd相切时上端偏离O′最远,由几何关系可得:O′P=
当α粒子运动的圆轨迹与cd相切时上端偏离O′最远,由几何关系可得:O′P=| R2-(R-s)2 |
将数据代入②式可得:O′P=0.16m
当α粒子沿Sb方向射入时,下端偏离O′最远,由几何关系可得:O′Q=
| R2-(R-s)2 |
将数据代入②式可得:O′Q=0.16m
故金箔被α粒子射中区域的长度为:
y=O′P+O′Q=0.31m…④
(2)如图所示,OE为α粒子绕O点做圆周运动的半径r,α粒子在无场区域内做直线运动与MN相交,下偏距离为y′,
因为R=0.2m,L=0.12m,O′Q=0.16m,
所以sinα=
| L |
| R |
y′=Ltan37°…⑤
所以圆周运动的半径为:r=
| y′+Q′Q |
| cos37° |
将数据代入⑥式可得:r=0.31m…⑦
即|OE|的长度为0.31m.
(3)设α粒子穿出金箔时的速度为v′,由牛顿第二定律可得:k
| r2 |
| v′2 |
| r |
α粒子从金箔穿出时损失的动能为△Ek,则:
△Ek=
| 1 |
| 2 |
| 1 |
| 2 |
由⑨式可得:△Ek=2.5×10-14J…⑩
答:
(1)金箔cd被α粒子射中区域的长度y值是0.31m;
(2)
. |
| OE |
(3)此α粒子从金箔穿出时损失的动能是2.5×10-14J.
点评:本题是带电粒子在组合场中运动的问题,解题关键是画出粒子的运动轨迹,运用几何知识求解轨迹半径和OE的长度.

练习册系列答案
相关题目
 (2010?肇庆一模)如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开.当K接通时,以下说法中正确的是( )
(2010?肇庆一模)如图所示,理想变压器的输入端接正弦交流电,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开.当K接通时,以下说法中正确的是( )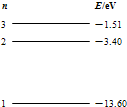 (2010?肇庆一模)使某种金属X发生光电效应所需的光子最小的能量为2.60eV.已知一群氢原子处于量子数n=3的激发态,其能级如右图所示.这些氢原子能够自发地跃迁到较低的能量状态,并向外辐射多种频率的光.那么,若用这些氢原子辐射的光照射这种金属,能够使这种金属X发生光电效应的有几种不同频率的光( )
(2010?肇庆一模)使某种金属X发生光电效应所需的光子最小的能量为2.60eV.已知一群氢原子处于量子数n=3的激发态,其能级如右图所示.这些氢原子能够自发地跃迁到较低的能量状态,并向外辐射多种频率的光.那么,若用这些氢原子辐射的光照射这种金属,能够使这种金属X发生光电效应的有几种不同频率的光( )