题目内容

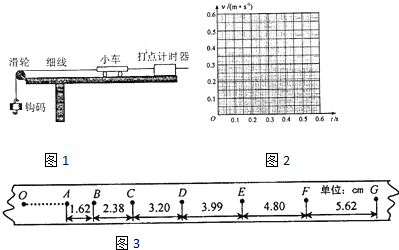
如图1所示，一打点计时器固定在斜面上端，一小车拖着穿过打点计时器的纸带从斜面上滑下．如图2是打出的纸带的一段，由于实验者粗心，不小心把纸带弄成了三段，但幸好找到了最初和最后两段，中间一段丢失了．已知打点计时器使用的交流电频率为50Hz，即下图每两个计时点的时间间隔为0.02秒．根据如图给出的数据．

（1）计算小车通过A点的速度vA=
1.36
1.36
m/s．
（2）计算小车通过B点的速度vB=
2.29
2.29
m/s．
（3）计算小车的加速度a=
3.87
3.87
m/s2．
（4）丢失的中间一段纸带上应该有
3
3
个计时点（填阿拉伯数字）．
分析：根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上A点时小车的瞬时速度大小．
解答：解：（1）在A点左方5.12cm到右方5.74cm这段距离内，A点是中间时刻．匀变速直线运动中间时刻速度等于该过程中的平均速度，
即：vA=
(0.0512+0.0574)m
0.08s
=1.36m/s
（2）在B点左方8.85cm到右方9.47cm这段距离内，B点是中间时刻．匀变速直线运动中间时刻速度等于该过程中的平均速度，
即：vB=
(0.0885+0.0947)m
0.08
=2.29m/s
（3）任意选取相邻的两段位移，比如：8.58cm和9.47cm的两段纸带，
根据匀变速直线运动的推论公式△x=aT2
得：a=3.87m/s2
（4）匀变速直线运动连续相等时间内的位移之差：
x2-x1=△x=aT2=0.61cm    ①
匀变速直线运动不连续相等时间内的位移之差：
xm-xn=(m-n)△x=(m-n)aT2=8.24cm-6.37cm=1.87cm   ②
由①②两式可知：3△x=1.87cm
所以丢失的中间一段纸带上应该有3个计数点．
答：计算小车通过A点的速度vA为1.36m/s；计算小车通过B点的速度vA为2.29m/s；小车的加速度a为a=3.87m/s2；丢失的中间一段纸带上应该有3个计数点．
点评：本题考查了“探究匀变速直线运动”的实验中所需实验器材，以及利用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用，提高解决问题能力．
练习册系列答案
相关题目
小华同学在做“研究匀变速直线运动”实验中，将打点计时器固定在某处，在绳子拉力的作用下小车拖着穿过打点计时器的纸带在水平木板上运动，如图1所示．由打点计时器得到表示小车运动过程的一条清晰纸带的一段．
如图2所示，在打点计时器打出的纸带上确定出八个计数点，相邻两个计数点之间的时间间隔为0.1s，并用刻度尺测出了各计数点到0计数点的距离，图中所标数据的单位是cm．
（1）根据纸带提供的信息，小华同学已经计算出了打下1、2、3、4、5这五个计数点时小车的速度，请你帮助他计算出打下计数点6时小车的速度（结果保留3位有效数字），并填入下表．
计数点 1 2 3 4 5 6
t/s 0.1 0.2 0.3 0.4 0.5 0.6
v/（m．s） 0.358 0.400 0.440 0.485 0.530
0.57
0.57
（2）以速度v为纵轴、时间t为横轴在坐标纸上建立直角坐标系，根据上表中的v、t数据，在坐标系中描点，并作出小车运动的图3．
（3）根据v-t图象可知，在打0计数点时，小车的速度v0=
0.310
0.310
m/s（保留3位有效数字）；小车运动的加速度为
0.43
0.43
m/s2（保留2位有效数字）．
小华同学在做“研究匀变速直线运动”实验时，从打下的若干纸带中选出了如图1所示的一条纸带，已知打点计时器使用电源频率为50Hz，每两个相邻计数点间有四个点没有画出，各计数点到0点的距离如纸带上所示，

（1）为了达到实验的目的，除了有电磁打点计时器、纸带、小车、细绳、导线、低压交流电源、小木块、长木板外，还需要的仪器有
A
A

A．刻度尺 　　　B．铁架台　　　　C．秒表　　　　D．天平
（2）图中两计数点的时间间隔为T=
0.1
0.1
s
（3）根据纸带提供的信息，小华同学已经计算出了打下1、2、3、4、6这五个计数点时小车的速度，请你帮助他计算出打下计数点5时小车的速度v5=
0.530
0.530
m/s（结果保留3位有效数字），并填入下表．
计数点 1 2 3 4 5 6
t/s 0.1 0.2 0.3 0.4 0.5 0.6
v/（m?s-1） 0.358 0.400 0.440 0.485
0.530
0.530
 0.575
（4）以速度v为纵轴、时间t为横轴在坐标纸上建立直角坐标系，根据上表中的v、t数据，在如图2坐标系中描点，并作出小车运动的v-t图象．
（5）根据v-t图象可知，小车运动的加速度大小为
0.430
0.430
m/s2（结果保留3位有效数字）
实验
I．某物理兴趣小组在一次探究活动中，要测量滑块与木板之间的动摩擦因数．实验装置如图1所示，一表面粗糙的木板固定在水平桌面上，右端装有定滑轮；木板上有一滑块，其左端与穿过电磁打点计时器的纸带相连，右端通过跨过定滑轮的细线与托盘连接．打点计时器使用的交流电源频率为50Hz．开始实验时，在托盘中放入适量砝码，滑块开始做匀加速直线运动，在
纸带上打出一系列点．
（1）图2给出的是实验中获取纸带的一部分：0、1、2、3、4、5、6是计数点，每相邻两计数点间还有4个打点（图中未标出），用刻度尺测量出计数点间的距离如图所示．根据图中数据计算的加速度a=
0.497m/s2
0.497m/s2
（保留三位有效数字）．
（2）请回答下列两个问题：
①为了测量滑块与木板之间的动摩擦因数，还需测量的物理量是
CD
CD
（填写字母代号）
A．木板的长度L            B．木板的质量m1       C．滑块的质量m2
D．托盘和砝码的总质量m3   E．滑块的运动时间t
②欲测量①中所选定的物理量，所需要的实验器材是
天平
天平
．
（3）实验时，用托盘和砝码的总重力来代替细绳对滑块的拉力，则滑块与木板间的动摩擦因数μ=
m3g-m2a
m2g
m3g-m2a
m2g
 （用L、g、a、
m1、m2、m3、t中所需要的字母表示）．与真实值相比，测量的动摩擦因数
偏大
偏大
 （填“偏大”或“偏小”）．
II．在“互成角度的两个力的合成”实验中，如图3所示，用AB两弹簧秤拉橡皮条结点O，使其位于E处，此时α+β=90°，然后保持A的读数不变，当α角由图3中所示的值逐渐减小时，要使结点仍在E处，可采取的办法是
B
B

A．增大B的读数，减小β角
B．减小B的读数，减小β角
C．减小B的读数，增大β角
D．增大B的读数，增大β角．
如图1所示，将打点计时器固定在铁架台上，使重物带动纸带从静止  开始自由下落，利用此装置可以测定重力加速度．
（1）所需器材有：电火花打点计时器、纸带、墨粉纸盘、带铁夹的铁架台和带夹子的重物，此外还需
CD
CD
（填字母代号）中的器材．
A．直流电源   B．天平及砝码   C．交流电源       D．毫米刻度尺
（2）下列实验操作步骤正确的是
B
B

A．实验所用的重物可用实心泡沫球
B．应调整打点计时器，使其两限位孔连线在竖直方向
C．实验时应先使重物靠近打点计时器再释放，释放后再接通电源
（3）实验中得到的一条纸带如图2所示，从比较清晰的点起，每2个打印点取一个点作为计数点，分别标明0，1，2，3，4．测得x1=30.0mm，x2=45.4mm，x3=60.8mm，x4=76.2mm，则物体在打下点2时的速度大小为
0.9425
0.9425
m/s．物体的加速度大小为
9.625
9.625
m/s2．该实验中测得的重力加速度偏小，其主要原因是
实验中存在摩擦阻力
实验中存在摩擦阻力
．
某同学在“探究小车速度随时间变化规律”的活动中，如图1所示，用打点计时器记录被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点，其相邻点间的距离如图3所示，每个相邻的计数点间的时间间隔为0.10s．
精英家教网
（1）按照实验进行的先后顺序，将下述步骤的代号填在横线上
 

A．把穿过打点计时器的纸带固定在小车的后面
B．把打点计时器固定在木板的没有滑轮的一端，并连好电路
C．换上新的纸带，再重做两次
D．把长木板平放在实验桌上，并使滑轮伸出桌面
E．使小车停在靠近打点计时器处，接通电源，放开小车，让小车运动
F．把一条细绳拴在小车上，细绳跨过定滑轮，下边吊着合适的钩码
G．断开电源，取出纸带
（2）试根据纸带上各个计数点间的距离，每隔0.10s测一次速度，计算出打下B、C、D、E、F五个点时小车的瞬时速度，并将各个速度值填入下表（结合纸带数据，选择从理论上看误差较小的方法计算瞬时速度．结果保留3位有效数字）
（3）从A点开始计时，将B、C、D、E、F各个时刻的瞬时速度描在直角坐标系中，如图2所示，并画出小车的瞬时速度（υ）随时间（t）的变化图线．
（4）根据画出的υ-t图线可得小车速度随时间变化的
规律是：
 
，
依据是：
 
．
（5）在实验中，甲同学选择用AD间的平均速度代替B点的瞬时速度，乙同学选用AC间的平均速度代替B点的瞬时速度，丙同学选用AB间的平均速度代替B点的瞬时速度，你认为三位同学中比较准确的是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网