题目内容
篮球比赛时,为了避免对方运动员的拦截,往往采取将篮球与地面发生一次碰撞后传递给队友的方法传球.设运动员甲以 vo=5m/s 的水平速度将球从离地面高 h1=0.8m 处抛出,球与地面碰撞后水平方向的速度变为原来水平速度的 4/5,竖直方向离开地面的瞬间的速度变为与地面碰前瞬间竖直方向速度的 3/4,运动员乙恰好在篮球的速度变为水平时接住篮球,篮球的质量 m=0.5kg,与地面碰撞作用的时间 t=0.02s,运动员与篮球均可看成质点,不计空气阻力,篮球与地面接触时可看成是水平方向的匀变速运动,g 取 10m/s2,求:(1)甲抛球的位置与乙接球的位置之间的水平距离 s
(2)球与地面间的动摩擦因数 μ
【答案】分析:(1)甲抛球的位置与乙接球的位置之间的水平距离由三段位移构成,球与地面撞击前的平抛运动的水平射程、球与地面撞击过程中的水平位移、球与地面撞击后的斜抛运动(可反演为平抛运动)的水平射程.分别根据平抛运动的知识和匀变速直线运动的规律求解.
(2)在球与地面撞击过程中,在竖直方向上运用动量定理求出球与地面碰撞时的弹力FN,在水平方向上运用动量定理求出球与地面碰撞时的摩擦力f,再根据f=μFN求解动摩擦因数.
解答: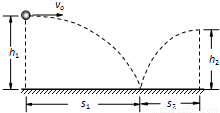 解:(1)依题意画出如图 所示:
解:(1)依题意画出如图 所示:
∵t1=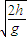 =
=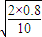 =0.4 s
=0.4 s
∴s1=vot1=5×0.4=2 m
球与地碰前瞬间竖直方向的速度:
v1=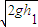 =
=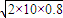 =4 m/s
=4 m/s
碰后瞬间竖直方向的速度 v2= v1=
v1= ×4=3 m/s
×4=3 m/s
∴t2=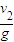 =
=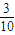 =0.3 s
=0.3 s
与地碰后水平方向的速度 vo′=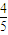 vo=
vo=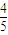 ×5=4 m/s
×5=4 m/s
∴s2=vo′t2=4×0.3=1.2 m
而球与地面接触时的位移为:s3= (vo+vo′)t=
(vo+vo′)t= ×(5+4)×0.02=0.09 m
×(5+4)×0.02=0.09 m
∴s=s1+s2+s3=2+1.2+0.09=3.29 m
(2)球与地面碰撞时的弹力为:(FN-mg)t=m v2-m(-v1)
解得 FN=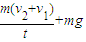 =
=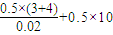 =180 N
=180 N
球与地面碰撞时的摩擦力为 f,由动量定理,有:-f t=m vo′-m vo
解得 f=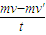 =
=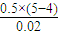 =25 N
=25 N
∴μ=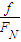 =
=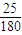 ≈0.14
≈0.14
答:(1)甲抛球的位置与乙接球的位置之间的水平距离为3.29m.
(2)球与地面间的动摩擦因数为0.14.
点评:此题要求对球的运动过程分析清楚:碰撞前的平抛运动、碰撞过程的匀变速运动、碰撞后的斜抛运动.在碰撞中,分别要在竖直方向和水平方向上运用动量定理.此题有一定的难度,属于难题.
(2)在球与地面撞击过程中,在竖直方向上运用动量定理求出球与地面碰撞时的弹力FN,在水平方向上运用动量定理求出球与地面碰撞时的摩擦力f,再根据f=μFN求解动摩擦因数.
解答:
 解:(1)依题意画出如图 所示:
解:(1)依题意画出如图 所示:∵t1=
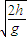 =
=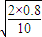 =0.4 s
=0.4 s ∴s1=vot1=5×0.4=2 m
球与地碰前瞬间竖直方向的速度:
v1=
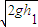 =
=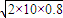 =4 m/s
=4 m/s 碰后瞬间竖直方向的速度 v2=
 v1=
v1= ×4=3 m/s
×4=3 m/s ∴t2=
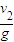 =
=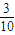 =0.3 s
=0.3 s 与地碰后水平方向的速度 vo′=
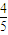 vo=
vo=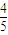 ×5=4 m/s
×5=4 m/s ∴s2=vo′t2=4×0.3=1.2 m
而球与地面接触时的位移为:s3=
 (vo+vo′)t=
(vo+vo′)t= ×(5+4)×0.02=0.09 m
×(5+4)×0.02=0.09 m ∴s=s1+s2+s3=2+1.2+0.09=3.29 m
(2)球与地面碰撞时的弹力为:(FN-mg)t=m v2-m(-v1)
解得 FN=
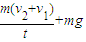 =
=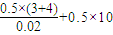 =180 N
=180 N 球与地面碰撞时的摩擦力为 f,由动量定理,有:-f t=m vo′-m vo
解得 f=
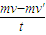 =
=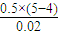 =25 N
=25 N ∴μ=
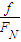 =
=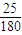 ≈0.14
≈0.14 答:(1)甲抛球的位置与乙接球的位置之间的水平距离为3.29m.
(2)球与地面间的动摩擦因数为0.14.
点评:此题要求对球的运动过程分析清楚:碰撞前的平抛运动、碰撞过程的匀变速运动、碰撞后的斜抛运动.在碰撞中,分别要在竖直方向和水平方向上运用动量定理.此题有一定的难度,属于难题.

练习册系列答案
相关题目

 =5m/s的水平速度将球从离地面高h1=0.8m处抛出,球与地面碰撞后水平方向的速度变为原来水平速度的
=5m/s的水平速度将球从离地面高h1=0.8m处抛出,球与地面碰撞后水平方向的速度变为原来水平速度的 ,竖直方向离开地面的瞬间的速度变为与地面碰前瞬间竖直方向速度的
,竖直方向离开地面的瞬间的速度变为与地面碰前瞬间竖直方向速度的 ,运动员乙恰好在篮球的速度变为水平时接住篮球,篮球的质量m=0.5kg,与地面碰撞作用的时间t=0.02s,运动员与篮球均可看成质点,不计空气阻力,篮球与地面接触时可看成是匀变速运动,g取10m/s2,求:
,运动员乙恰好在篮球的速度变为水平时接住篮球,篮球的质量m=0.5kg,与地面碰撞作用的时间t=0.02s,运动员与篮球均可看成质点,不计空气阻力,篮球与地面接触时可看成是匀变速运动,g取10m/s2,求: