题目内容
如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=15m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数μ=0.5，取g=10m/s2，求：（1）物块与小车保持相对静止时的速度大小v；
（2）物块在车面上滑行的时间t；
（3）要使物块不从小车右端滑出，物块滑上小车左端的速度
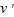不超过多少．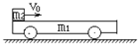
【答案】分析：（1）由于摩擦作用，滑块减速，平板小车加速，系统水平方向不受外力，总动量守恒，可求出相对静止时的共同速度；
（2）对小车运用动量定理求解出加速时间．
（3）要使物块恰好不从小车右端滑出，滑块滑到小车的最右端，两者速度相同，根据能量守恒求解速度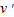
．
解答：解：
（1）依据动量守恒得 m2v=（m1+m2）v
解得 v=0.8m/s
（2）物块所受的滑动摩擦力大小f=μm2g=1N
对小车，依据动量定理得 ft=m1v
解得t=0.24s
（3）依据动量守恒有：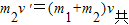
依据能量关系有：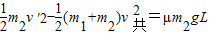
解得 v′=5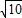
m/s
则要使物块不从小车右端滑出，必须满足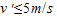
答：
（1）物块与小车保持相对静止时的速度大小v为0.8m/s；
（2）物块在车面上滑行的时间t是0.24s；
（3）要使物块不从小车右端滑出，物块滑上小车左端的速度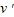
不超过5m/s．
点评：本题关键是根据动量守恒定律、动量定理、能量守恒列式求解，也可以根据牛顿第二定律和速度时间公式列式联立求解．
（2）对小车运用动量定理求解出加速时间．
（3）要使物块恰好不从小车右端滑出，滑块滑到小车的最右端，两者速度相同，根据能量守恒求解速度
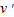．解答：解：
（1）依据动量守恒得 m2v=（m1+m2）v
解得 v=0.8m/s
（2）物块所受的滑动摩擦力大小f=μm2g=1N
对小车，依据动量定理得 ft=m1v
解得t=0.24s
（3）依据动量守恒有：
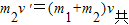
依据能量关系有：
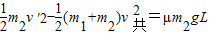
解得 v′=5
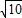m/s则要使物块不从小车右端滑出，必须满足
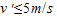
答：
（1）物块与小车保持相对静止时的速度大小v为0.8m/s；
（2）物块在车面上滑行的时间t是0.24s；
（3）要使物块不从小车右端滑出，物块滑上小车左端的速度
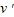不超过5m/s．点评：本题关键是根据动量守恒定律、动量定理、能量守恒列式求解，也可以根据牛顿第二定律和速度时间公式列式联立求解．
练习册系列答案
相关题目
如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=15m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v0=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数=0.5，取g=10m/s2．求
（2009?天津）如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=1.5m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v0=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数μ=0.5，取g=10m/s2，求
如图所示，质量m1=20kg和m2=50kg的两物体，叠放在动摩擦因数为0.40的粗糙水平地面上，一处于水平位置的轻弹簧，劲度系数为200N/m，一端固定于墙壁，另一端与质量为m1的物体相连，弹簧处于自然状态，现用一水平推力F作用于质量为m2的物体上，使它缓慢地向墙壁一侧移动，取g=10m/s2，当移动0.50m时，两物体间开始相对滑动，这时水平推力F的大小为（ ）
如图所示，质量m1=1g、带电量q1=+5×10-7C的小金属块位于绝缘水平面上，匀强电场斜向上与水平面的夹角为53°．现将m1从A点由静止释放经时间t=1s到达B点与处于静止状态的另一带电量q2=-5×10-7C、质量m2=5g的小金属块相碰，碰后m1向左又滑行了S1=0.4m后停下．AB间的距离为L=1.5m，两金属块与水平面间的动摩因数均为μ=0.5，两金属块的库仑力忽略不计．
（2011?静安区二模）（A）某天文台测得某行星的一颗卫星绕行星做匀速圆周运动，测得其轨道半径为R，周期为T，则其向心加速度为