Question

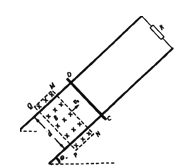
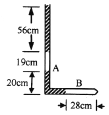
【题目】如图所示，L形直角细管，竖直部分管内两水银柱长度分别为56cm和20cm，竖直管和水平管各封闭了一段气体A和B，长度分别为19cm和28cm，且上端水银面恰至管口，外界大气压强为76mHg．现以水平管为轴缓慢转动使L形管变为水平，此过程中气柱B的长度变为______cm，溢出的水银柱长度为______cm。

Answer 1

【答案】56； 42

【解析】

分别以上下各液柱为研究对象，由平衡可求得A、B内气体的压强；L水平后两部分气体的压强都应等于大气压强，则由玻意耳定律可得出气体长度的变化，得出溢出的水银长度．

由图可知，A中的气体压强PA=（76+56）cmHg=132cmHg；
B中气体压强PB=（132+20）cmHg=152cmHg；
L形管变为水平后，两部分气体压强均等于大气压强P=76mcHg；
由玻意耳定律可知：PBLBS=PLB′S；
PALAS=PLA′S；
代入以上数据解得：LA′=33cm； LB′=56cm；
故A气体长度增加了33-19cm=14cm； B中气体长度增加56-28=28cm；
溢出的水银长度为14+28cm=42cm；