题目内容
 一对平行金属板水平放置,两板相距为d,在下板的下侧空间有垂直纸面水平向里的匀强磁场,磁感应强度为B,两板中心开有上下对应的两个小孔,当两板间加上电压V以后,带电量为+q.质量为m的两个相同质点,分别从两板间左端中点a和上板中心小孔b处同时飞人,由a点飞入的质点初速度为2v0,且方向平行金属板;由b飞人的质点初速度为v0,且方向垂直金褐板,结果两质点同时穿过下板的小孔C后,又分别在磁场中偏转,最后均打在下极板的下表面L(不计重力的影响,也不考虑两质点问的相互影响).求:
一对平行金属板水平放置,两板相距为d,在下板的下侧空间有垂直纸面水平向里的匀强磁场,磁感应强度为B,两板中心开有上下对应的两个小孔,当两板间加上电压V以后,带电量为+q.质量为m的两个相同质点,分别从两板间左端中点a和上板中心小孔b处同时飞人,由a点飞入的质点初速度为2v0,且方向平行金属板;由b飞人的质点初速度为v0,且方向垂直金褐板,结果两质点同时穿过下板的小孔C后,又分别在磁场中偏转,最后均打在下极板的下表面L(不计重力的影响,也不考虑两质点问的相互影响).求:(1)两质点在金属板间运动的时间t1.
(2)两质点在磁场中运动的时间ta和tb
(3)两质点在下板的下表耐上撞击点间的距离△s.
分析:从a 点飞入电场的质点做类平抛运动,结合条件运用平抛运动规律可求出运动时间及速度.从b点飞入电场的质点做匀加速直线运动,由条件结合运动学公式可求出运动的时间及速度.
从b点飞入的质点由C点飞出后被磁场偏转后又打到下极板.由各自的速度、带电量及质量可求出各自的运动半径,从而可算出两质点在下板的下表耐上撞击点间的距离△s.
从b点飞入的质点由C点飞出后被磁场偏转后又打到下极板.由各自的速度、带电量及质量可求出各自的运动半径,从而可算出两质点在下板的下表耐上撞击点间的距离△s.
解答:解:(1)a做类平抛运动,竖直方向:
=
at2
b向下匀加速运动,则有d=v0t+
at2
由牛顿第二定律可得:
=ma
则有t=
=
(2)在磁场中两个质点均做匀速圆周运动,且由qvB=m
和 T=
得
Ta=Tb=
a质点飞入磁场与水平方向角度 tanθ=
=1 得θ=45°
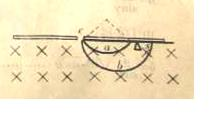
则a在B中运动时间:ta=
=
b在B中运动的时间为:tb=
=
(3)a质点在C处的速度为:va=
×2v0 运动半径:Ra=
则有sa=
Ra=
而b质点在C处的速度为:vb=v0+at=3v0
又Rb=
则有sb=2Rb=
所以△s=
.
| d |
| 2 |
| 1 |
| 2 |
b向下匀加速运动,则有d=v0t+
| 1 |
| 2 |
由牛顿第二定律可得:
| qU |
| d |
则有t=
| 2v0 |
| a |
| 2v0md |
| qU |
(2)在磁场中两个质点均做匀速圆周运动,且由qvB=m
| v2 |
| R |
| 2πR |
| v |
Ta=Tb=
| 2πm |
| qB |
a质点飞入磁场与水平方向角度 tanθ=
| at |
| 2v0 |

则a在B中运动时间:ta=
| T |
| 4 |
| πm |
| 2Bq |
b在B中运动的时间为:tb=
| T |
| 2 |
| πm |
| Bq |
(3)a质点在C处的速度为:va=
| 2 |
| mv0 |
| Bq |
则有sa=
| 2 |
| 4mv0 |
| Bq |
而b质点在C处的速度为:vb=v0+at=3v0
又Rb=
| mvb |
| Bq |
则有sb=2Rb=
| 6mv0 |
| Bq |
所以△s=
| 2mv0 |
| Bq |
点评:带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径.在电场中做类平抛运动,将运动分解成相互垂直的两方向.

练习册系列答案
相关题目
 一对平行金属板水平放置,板间距离为d=0.5米,板间有磁感应强度为B=5T的水平向里的匀强磁场,将金属板连入如图所示的电路,已知电源内阻为r=10Ω,滑动变阻器的总电阻为R=40Ω,现将开关S闭合,并调节滑动触头P至右端长度为总长度的
一对平行金属板水平放置,板间距离为d=0.5米,板间有磁感应强度为B=5T的水平向里的匀强磁场,将金属板连入如图所示的电路,已知电源内阻为r=10Ω,滑动变阻器的总电阻为R=40Ω,现将开关S闭合,并调节滑动触头P至右端长度为总长度的
 处,一质量为m、电荷量为q的带电质点从两板正中央左端以某一初速度水平飞入场区,恰好做匀速圆周运动.
处,一质量为m、电荷量为q的带电质点从两板正中央左端以某一初速度水平飞入场区,恰好做匀速圆周运动.
 处,一质量为m、电荷量为q的带电质点从两板正中央左端以某一初速度水平飞入场区,恰好做匀速圆周运动.
处,一质量为m、电荷量为q的带电质点从两板正中央左端以某一初速度水平飞入场区,恰好做匀速圆周运动. 