题目内容
如图所示,两根平行光滑金属导轨MP、NQ与水平面成θ=37°角固定放置,导轨电阻不计,两导轨间距L="0.5" m,在两导轨形成的斜面上放一个与导轨垂直的均匀金属棒ab,金属棒ab处于静止状态,它的质量为
 。金属棒ab两端连在导轨间部分对应的电阻为R2=2Ω,电源电动势E=2V,电源内阻r=1Ω,电阻R1=2Ω,其他电阻不计。装置所在区域存在一垂直于斜面MPQN的匀强磁场。(已知sin37°=0.6,cos37°=0.8,
。金属棒ab两端连在导轨间部分对应的电阻为R2=2Ω,电源电动势E=2V,电源内阻r=1Ω,电阻R1=2Ω,其他电阻不计。装置所在区域存在一垂直于斜面MPQN的匀强磁场。(已知sin37°=0.6,cos37°=0.8, )求:
)求:

(1)所加磁场磁感应强度方向;
(2)磁感应强度B的大小。
【答案】
(1)垂直斜面向下(2)0.6T
【解析】
试题分析:(1)金属棒ab处于静止状态,受安培力必沿斜面向上,由左手定则可得,所加磁场磁感应强度方向垂直斜面向下。
(2)由图可知 与
与 并联,总电阻
并联,总电阻
电路中的总电流
通过导体棒的电流
导体棒受到安培力为
由平衡条件有
解得磁感应强度为B=0.6T
考点:安培力
点评:应用平衡条件解决磁场中导体的平衡问题,关键在于安培力的分析和计算,在匀强磁场中,当通电导体与磁场垂直时,安培力大小F=BIL,方向由左手定则判断。

练习册系列答案
相关题目
 (2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )
(2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )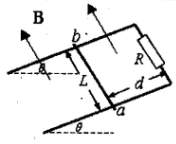 (1)如图所示,两根足够长、电阻不计的光滑平行金属导轨相距为L=lm,导轨平面与水平面成θ=30°角,上端连接R=1.5Ω的电阻,质量为m=0.2kg、阻值r=0.5Ω的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d=4m,整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.
(1)如图所示,两根足够长、电阻不计的光滑平行金属导轨相距为L=lm,导轨平面与水平面成θ=30°角,上端连接R=1.5Ω的电阻,质量为m=0.2kg、阻值r=0.5Ω的金属棒ab放在两导轨上,与导轨垂直并接触良好,距离导轨最上端d=4m,整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.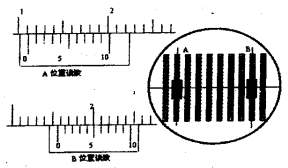
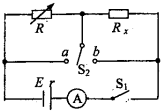
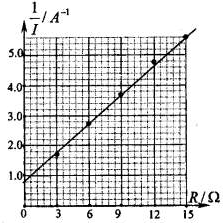
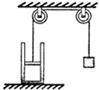 (2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.
(2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.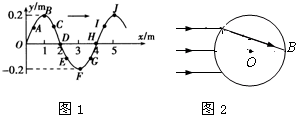 (3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为
(3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为
 ,既适用于声波也适用于光波
,既适用于声波也适用于光波

 +
+ →
→ B.
B. +
+
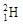 +
+ →
→ D.
D. →
→
 ,真空中的光速为
,真空中的光速为 ,普朗克常量为
,普朗克常量为 ,则每一个光子的动量为 ;该激光器在
,则每一个光子的动量为 ;该激光器在 秒内辐射的光子数为 。
秒内辐射的光子数为 。


