题目内容
海水中含有大量的带电离子，日本的一些科学家曾设想利用流动的海水建造一座磁流体发电机．图示为该磁流体发电机的原理示意图，上、下两块金属板M、N水平放置浸没在海水里，金属板面积均为S=1×103m2，板间相距d=100m，海水的电阻率ρ=0.25Ω?m．在金属板之间加一匀强磁场，磁感应强度B=0.1T，方向由南向北，海水从东向西以速度v=5m/s流过两金属板之间时，将在两板之间形成电势差，则（1）达到稳定状态时，哪块金属板的电势较高？
（2）由金属板和海水流动所构成的电源的电动势E和等效内阻r各为多少？
（3）若用此发电装置给一电阻为20Ω的航标灯供电，则在8h内航标灯所消耗的电能为多少？
【答案】分析：（1）根据左手定则，即可求解；
（2）根据电场力等于洛伦兹力，结合电阻定律，即可求解；
（3）根据闭合电路欧姆定律，与焦耳定律，即可求解．
解答：解：
（1）根据左手定则可确定N板电势高．?
（2）设海水中带电离子电量大小为q，达到稳定状态时，离子受到的电场力和洛伦兹力平衡，则有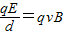
∴E=Bvd=50V
电流从M流向N，其等效内阻为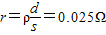
（3）此电源给航标灯供电时，电路中电流为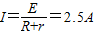
航标灯所消耗的电能为 Q=I2Rt=3.6×106J
答：（1）达到稳定状态时，N金属板的电势较高；
（2）由金属板和海水流动所构成的电源的电动势50V和等效内阻r0.025Ω
（3）若用此发电装置给一电阻为20Ω的航标灯供电，则在8h内航标灯所消耗的电能为3.6×106J．
点评：考查左手定则、电阻定律、闭合电路欧姆定律与焦耳定律的应用，注意左手定则与右手定则的区别，分清电阻的长度与宽度．
（2）根据电场力等于洛伦兹力，结合电阻定律，即可求解；
（3）根据闭合电路欧姆定律，与焦耳定律，即可求解．
解答：解：
（1）根据左手定则可确定N板电势高．?
（2）设海水中带电离子电量大小为q，达到稳定状态时，离子受到的电场力和洛伦兹力平衡，则有
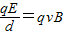
∴E=Bvd=50V
电流从M流向N，其等效内阻为
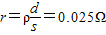
（3）此电源给航标灯供电时，电路中电流为
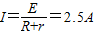
航标灯所消耗的电能为 Q=I2Rt=3.6×106J
答：（1）达到稳定状态时，N金属板的电势较高；
（2）由金属板和海水流动所构成的电源的电动势50V和等效内阻r0.025Ω
（3）若用此发电装置给一电阻为20Ω的航标灯供电，则在8h内航标灯所消耗的电能为3.6×106J．
点评：考查左手定则、电阻定律、闭合电路欧姆定律与焦耳定律的应用，注意左手定则与右手定则的区别，分清电阻的长度与宽度．
练习册系列答案
相关题目
海水中含有大量的带电离子，日本的一些科学家曾设想利用流动的海水建造一座磁流体发电机．图示为该磁流体发电机的原理示意图，上、下两块金属板M、N水平放置浸没在海水里，金属板面积均为S=1×103m2，板间相距d=100m，海水的电阻率ρ=0.25Ω?m．在金属板之间加一匀强磁场，磁感应强度B=0.1T，方向由南向北，海水从东向西以速度v=5m/s流过两金属板之间时，将在两板之间形成电势差，则
由于受到地球信风带和盛西风带的影响，在海洋中形成一种河流称为海流．海流中蕴藏着巨大的动力资源．据统计，世界大洋中所有海流的发电能力达109kW．因为海水中含有大量的带电离子，这些离子随海流作定向运动，如果有足够强的磁场能使正、负离子向相反方向偏转，便能发出电来．如图所示为该发电机的原理示意图，上、下两块金属板M，N水平放置浸没在海水里，金属板面积为S，在金属板之间加一匀强磁场，方向由南向北，海水从东向西流过两金属板之间，在两板之间形成电势差．下列说法正确的是（ ）| A、金属板N为发电机的正极 | B、当其它条件不变时，电动势E与板长L成正比 | C、当其它条件不变时，电动势E与两板的正对面积S成正比 | D、电动势E的大小还与海水的电阻率有关 |
，宽为
，两板间的距离为
，将管道沿风海流方向固定在风海流中，在金属板之间加一水平匀强磁场，磁感应强度大小为
，方向由南向北，用导线将M、N外侧连接电阻为
的航标灯（图中未画出）。工作时，海水从东向西流过管道，在两金属板之间形成电势差，可以对航标灯供电，设管道内海水的流速处处相同，且速率恒为
，海水的电阻率为
，海水所受摩擦力与流速成正比，比例系数为
。
的大小，并判断M、N两板哪个板电势较高；
时间内磁流体发电机消耗的总机械能。
