Question

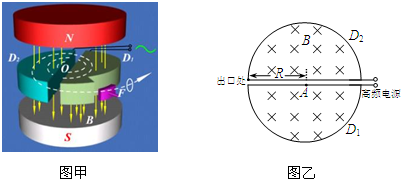
如图甲所示，在场强大小为E、方向竖直向下的匀强电场内存在一个半径为R的圆形区域，O点为该圆形区域的圆心，A点是圆形区域的最高点，B点是圆形区域最右侧的点．在A点由放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷，电荷的质量为m，电量为q，不计电荷的重力．
（1）正电荷以多大的速率发射，才能经过图中的P点（图甲中θ为已知）？
（2）在问题（1）中，电荷经过P点的动能是多大？
（3）若在圆形区域的边缘有一接收屏CBD，其中C、D分别为接收屏上最边缘的两点（如图乙所示），且∠COB=∠BOD=30°．则该屏上接收到的正电荷的最大动能是多少？

Answer 1

【答案】分析：（1）正电荷q做类平抛运动，将运动分解成水平方向匀速运动和竖直方向初速度为0的匀加速运动，再列出等式求解．
（2）对电荷从A到P点过程，运用动能定理求解电荷经过P点的动能．
（3）根据（2）题中的P点的动能的表达式求出当θ为何值时动能最大，并求解．
解答：解：（1）对正电荷q做类平抛运动
Rsinθ=Vt
R（1+cosθ）=
解得  v=
（2）对电荷从A到P点过程，运用动能定理得：
E_K-mV²=EqR（1+cosθ）
解得E_K=EqR（5+3cosθ）
（3）由上问结果可知当θ=60时，即电荷打到D点其动能最大
最大动能为：
E_Km=EqR（5+3cos60°）=
答：（1）正电荷以的速率发射，才能经过图中的P点
（2）在问题（1）中，电荷经过P点的动能是EqR（5+3cosθ）
（3）该屏上接收到的正电荷的最大动能是
点评：本题考查灵活选择解题规律的能力．类平抛运动通常用动力学方法处理，即电场强度方向做匀加速直线运动，垂直电场强度方向做匀速直线运动．