题目内容
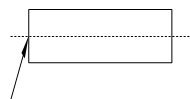
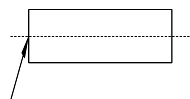
如图为一均匀的柱形透明体，折射率n=2．①求光从该透明体射向空气时的临界角；
②若光从空气中入射到透明体端面的中心上，试证明不 论入射角为多大，进入透明体的光线均不能从侧面“泄漏出去”．
【答案】分析：根据sinC=
求出光从该透明体射向空气时的临界角．当 入射角等于90度时，在端面处的折射角最大，则在侧面上的入射角最小，若能发生全反射，则不管入射角多大，进入透明体的光线均不能从侧面“泄漏出去”．
解答：解：①根据sinC=
得，
临界角
②证明：∵
∴当
最小
∵θ3＞C、∴任何光线均不能从侧面“泄漏出去”
点评：解决本题的关键掌握折射定律，抓住临界状态，运用折射定律和几何关系进行证明．
求出光从该透明体射向空气时的临界角．当 入射角等于90度时，在端面处的折射角最大，则在侧面上的入射角最小，若能发生全反射，则不管入射角多大，进入透明体的光线均不能从侧面“泄漏出去”．解答：解：①根据sinC=
得，临界角
②证明：∵
∴当
最小 ∵θ3＞C、∴任何光线均不能从侧面“泄漏出去”
点评：解决本题的关键掌握折射定律，抓住临界状态，运用折射定律和几何关系进行证明．
练习册系列答案
相关题目
如图为一均匀的柱形透明体，折射率n=2．
（选修3-4试题）
。
。