题目内容
如图所示，将质量m=1.24kg的圆环套在固定的水平直杆上，环的直径略大于杆的截面直径，环与杆的动摩擦因数μ=0.8。对环施加一位于竖直平面内斜向上与杆夹角θ=53°的恒定拉力F，使圆环从静止开始运动，第1s内前进了2m。（取g=10m/s²，sin53°=0.8，cos53°=0.6）
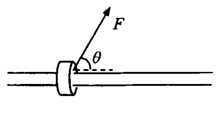
求：（1）圆环加速度a的大小；
（2）拉力F的大小。
【答案】
（1）4m/s2（2）当F<1.55N时大小为1.2N；当F>1.55N时大小为12.4N
【解析】
试题分析：（1）小环做匀加速直线运动，由运动学公式可知
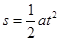则
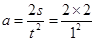m/s2
=4m/s2
（2）令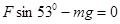
，F=1.55N
当F<1.55N时，环与杆上部接触，受力如图。
由牛顿第二定律可知
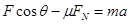
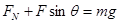
由此得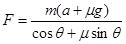
N=1.2N
当F>1.55N时，环与杆下部接触，受力如图
由牛顿第二定律可知
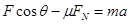
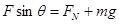
由此得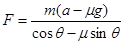
N=12.4N
考点：匀变速直线运动公式、牛顿运动定律
点评：此类题型属于高中物理比较典型的运动类型问题。通过匀变速直线运动规律求出加速度，然后利用正交分解法求出物体受力。在本题中还要涉及到由于F不一样，导致受力情况有两种，从而形成多解问题，需引起注意。
练习册系列答案
相关题目
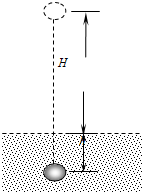如图所示，将质量m=2kg的一块石头从离地面H=2m高处由静止开始释放，落入泥潭并陷入泥中h=5cm深处，不计空气阻力，求泥对石头的平均阻力．
如图所示，将质量m=2kg的一个小钢球（可看成质点）从离地面H=2m高处由静止开始释放，落人泥潭并陷入泥中h=5cm深处，不计空气阻力（g取10m/s2），则下列说法正确的是（ ）
如图所示，将质量m=1kg的物体用两个劲度系数相同的弹簧竖直固定在升降机内，当升降机和物体一起静止时，上面弹簧对物体的弹力大小为1N；当它们一起以4m/s2的恒定加速度加速上升时，上面弹簧的弹力大小为（ ）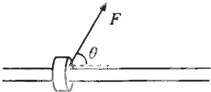
如图所示，将质量m=1.24kg的圆环套在固定的水平直杆上，环的直径略大于杆的截面直径，环与杆的动摩擦因数μ=0.8．对环施加一位于竖直平面内斜向上与杆夹角θ=53°的恒定拉力F，使圆环从静止开始运动，第1s内前进了2m．（取g=10m/s2，sin53°=0.8，cos53°=0.6）
如图所示，将质量M=1.20kg的小沙箱，用轻质软绳（不可伸长）悬挂起来，开始处于静止状态，绳的长度l=0.80m．用枪向沙箱发射质量m=0.05kg的子弹，子弹以v0=100m/s 的速度向右水平击中小沙箱，并留在小砂箱中，小沙箱在竖直平面内向上摆动．假设沙箱每次向左运动到最低点时就恰好有一颗同样速度的子弹射入沙箱，子弹射入沙箱的过程经历时间极短，可忽略不计，重力加速度g=10m/s2，不计空气阻力．