题目内容
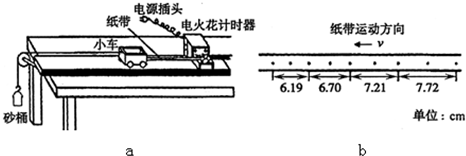
在“验证牛顿运动定律”实验中,所用的实验装置如图所示.在调整带滑轮木板的倾斜程度时,应使小车在不受牵引力时能拖动纸带沿木板匀速运动.小车的质量为M,盘和盘中重物的总质量为m,保持M不变,研究小车的加速度与力的关系时,在 条件下,mg近似等于小车运动时所受的拉力.实验中打出的一条纸带如下图所示,纸带上相邻两个计数点之间有四个实际点未画出,已知交流电频率为50HZ,AB=19.9mm,AC=49.9mm,AD=89.9mm,AE=139.8mm,则打该纸带时小车的加速度大小为 m/s2
(保留两位有效数字)

(保留两位有效数字)

分析:(1)根据牛顿第二定律,求出小车实际的拉力大小,然后和mg进行比较,可以得出结论;
(2)利用逐差法可以求出加速度的大小;
(2)利用逐差法可以求出加速度的大小;
解答:解:(1)根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
=
,由此可知当m<<M时,即当钩码的总重力要远小于小车的重力,绳子的拉力近似等于钩码的总重力.
故答案为:m<<M.
(2)根据匀变速直线运动的推论△x=aT2,有:
xCD-xAB=2a1T2 ①
xDE-xBC=2a2T2 ②
a=
③
联立①②③解得:a=
=
×10-3m/s2=1m/s2
故答案为:m<<M,1.0;
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
| mMg |
| m+M |
| mg | ||
1+
|
故答案为:m<<M.
(2)根据匀变速直线运动的推论△x=aT2,有:
xCD-xAB=2a1T2 ①
xDE-xBC=2a2T2 ②
a=
| a1+a2 |
| 2 |
联立①②③解得:a=
| xDE+xCD-xAB-xBC |
| 4T2 |
| (139.8-49.9)-49.9 |
| 4×0.12 |
故答案为:m<<M,1.0;
点评:对于实验问题首先要 明确实验原理,理解重要步骤的操作,熟练应用基本物理解决实验问题.

练习册系列答案
相关题目
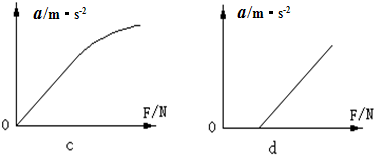
某同学在“验证牛顿运动定律”的实验中,保持小车所受的合力F的大小不变,改变小车的质量m,得到了不同m时的加速度大小a,并绘出了a-
的图象,则( )
| 1 |
| m |
| A、图象是一条直线,直线的斜率表示小车受到的合力的倒数 |
| B、图象是一条直线,直线的斜率表示小车受到的合力 |
| C、图象是一条曲线,曲线各点的切线斜率表示小车受到的合力的倒数 |
| D、图象是一条曲线,曲线各点的切线斜率表示小车受到的合力 |