题目内容
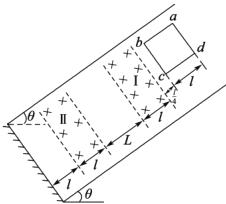
【题目】如图，一质量为m、边长为l的正方形金属线框abcd沿倾角为θ=30°的光滑斜面由静止下滑，依次经过宽度均为l的两匀强磁场区域Ⅰ和Ⅱ，下滑过程中，线框bc边一直与磁场边界平行，且金属线框bc边的初始位置离磁场Ⅰ的上边界的距离为
，两磁场的方向均垂直斜面向里，Ⅰ区域的磁感应强度是Ⅱ区域的磁感应强度的2倍。两磁场的间距为L（L未知，但L＞l），线框进入磁场Ⅰ时，恰好做匀速运动，从磁场I中穿出后又匀速通过磁场Ⅱ。重力加速度为g，求：
(1)在Ⅰ、Ⅱ两磁场中匀速运动时的速度大小的比值；
(2)写出L与l的关系式；
(3)若斜面底端离磁场Ⅱ下边界的距离为l，求金属线框从静止开始下滑到底端所产生的热量。
【答案】(1)1：4；(2)
；(3)2mgl。
【解析】
(1)金属线框进入磁场Ⅰ和Ⅱ后，均做匀速运动，据平衡条件有
mgsinθ=F安=BIl
线框切割磁感线时，电动势
E=Blv
线框中的电流
联立解得：
所以
；
(2)金属线框进入磁场Ⅰ前、离开磁场Ⅰ到进入磁场Ⅱ前，都是做匀加速直线运动，加速度为
a=gsinθ
由运动学公式
联立解得：
(3)产生的热量等于克服安培力做功
练习册系列答案
相关题目
