题目内容
 如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,将轨道固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小球与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小球质量m=0.01kg,轨道质量M=0.22kg,g=10m/s2,求:
如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,将轨道固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小球与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小球质量m=0.01kg,轨道质量M=0.22kg,g=10m/s2,求:(1)若v0=
| 21 |
(2)当v0至少为多大时,小球在最高点时才能使轨道对地面的压力为零.
分析:(1)对小球从a点到P点的过程由动能定理可求得小球在P点的速度;小球以此速度做平抛运动,由平抛运动的规律可求得水平射程;
(2)要使轨道对地面没有压力,则此时物体对轨道应有向上的弹力,大小等于轨道的重力;即此时轨道与小球的重力充当向心力;则有牛顿运动定律可求得P点的速度;再由动能定理可求得v0.
(2)要使轨道对地面没有压力,则此时物体对轨道应有向上的弹力,大小等于轨道的重力;即此时轨道与小球的重力充当向心力;则有牛顿运动定律可求得P点的速度;再由动能定理可求得v0.
解答:解:(1)设小球运动到最高点P的速度为v,根据动能定理有:
-μmgL-4mgR=m
①
v2=v02-2μgL-8gR ②
小球离开P点后做平抛运动,
则x轴:x=vt ③
y轴:4R=
④
联立解得:x=0.8m
(2)小球在最高点P时,要使轨道对地面压力为零,则小球在最高点速度为v,以整体为研究对象:
根据牛顿第二定律得:(M+m)g=m
⑤
又由动能定理可得:-μmgL-4mgR=m
⑥
解得:v0=6m/s
答:(1)小球从P点抛出后的射程为0.8m;(2)v0至少为6m/s时,轨道对地面才没有压力.
-μmgL-4mgR=m
v2
| ||
| 2 |
v2=v02-2μgL-8gR ②
小球离开P点后做平抛运动,
则x轴:x=vt ③
y轴:4R=
| gt2 |
| 2 |
联立解得:x=0.8m
(2)小球在最高点P时,要使轨道对地面压力为零,则小球在最高点速度为v,以整体为研究对象:
根据牛顿第二定律得:(M+m)g=m
| v2 |
| R |
又由动能定理可得:-μmgL-4mgR=m
v2-
| ||
| 2 |
解得:v0=6m/s
答:(1)小球从P点抛出后的射程为0.8m;(2)v0至少为6m/s时,轨道对地面才没有压力.
点评:本题考查动能定理及平抛运动和向心力公式,在解题时应注意明确物理过程,针对不同的过程灵活选用动能定理或机械能守恒列式.

练习册系列答案
相关题目

 轨道底端与水平地面相切。弹射装置将一个小球(可视为质点)从
轨道底端与水平地面相切。弹射装置将一个小球(可视为质点)从 点水平弹射向
点水平弹射向  点并进入轨道,经过轨道后从
点并进入轨道,经过轨道后从 点水平抛出,已知小物体与地面
点水平抛出,已知小物体与地面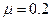 ,不计其它机械能损失,
,不计其它机械能损失, ,圆的半径
,圆的半径 ,小物体质量
,小物体质量 ,轨道质量为
,轨道质量为 ,
, ,求:
,求: ,小物体从
,小物体从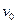 至少为多大时,可出现轨道对地面的瞬时压力为零。
至少为多大时,可出现轨道对地面的瞬时压力为零。