题目内容
 长1米的木板A,质量为M=1kg,静止在水平地面上.在木板最左端有一质量为m=2kg的小物块B,在沿水平向右F=10牛的恒力作用下由静止开始运动,物块和木板、木板和水平面间的滑动摩擦系数分别为μ1=0.2,μ2=0.1.在把小物块从木板右端拉下去的过程中,求:
长1米的木板A,质量为M=1kg,静止在水平地面上.在木板最左端有一质量为m=2kg的小物块B,在沿水平向右F=10牛的恒力作用下由静止开始运动,物块和木板、木板和水平面间的滑动摩擦系数分别为μ1=0.2,μ2=0.1.在把小物块从木板右端拉下去的过程中,求:(1)运动过程中A、B的加速度分别是多大?
(2)在此过程中木板运动的位移为多大?(小物块可看作质点)(g取10m/s2)
分析:根据牛顿第二定律分别求出木块和木板的加速度,根据运动学公式,抓住位移之差等于木板的长度求出运动的时间,从而求出木板运动的位移.
解答:解:(1)根据牛顿第二定律得,木块的加速度:a1=
=
=3m/s2
木板的加速度:a2=
=
=1m/s2
(2)由题意:
a1t2-
a2t2=L
得:t=1s
所以s2=
a2t2=
×1×12=0.5m;
答:(1)运动过程中A、B的加速度分别是3m/s2和1m/s2;
(2)在此过程中木板运动的位移为0.5m.
| F-μmg |
| m |
| 10-0.2×20 |
| 2 |
木板的加速度:a2=
| μ1mg-μ2(M+m)g |
| M |
| 0.2×20-0.1×(20+10) |
| 1 |
(2)由题意:
| 1 |
| 2 |
| 1 |
| 2 |
得:t=1s
所以s2=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)运动过程中A、B的加速度分别是3m/s2和1m/s2;
(2)在此过程中木板运动的位移为0.5m.
点评:解决本题的关键搞清木块木板的运动情况,抓住位移之差等于木板的长度,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
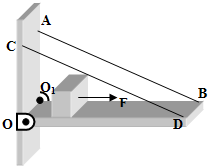 如图所示,质量不计、长度1米的轻质薄木板BDOO1被铰链和轻质细绳AB、CD水平地固定在竖直墙壁上,AB、CD与水平木板之间的夹角为30度,一重量为10牛顿的木块(可视为质点)置于木板的左端,木块与木板之间的摩擦系数为0.2,现对物块施加一水平向右的拉力F,F=7N,两根绳子各自能承受的最大拉力为9N,问:
如图所示,质量不计、长度1米的轻质薄木板BDOO1被铰链和轻质细绳AB、CD水平地固定在竖直墙壁上,AB、CD与水平木板之间的夹角为30度,一重量为10牛顿的木块(可视为质点)置于木板的左端,木块与木板之间的摩擦系数为0.2,现对物块施加一水平向右的拉力F,F=7N,两根绳子各自能承受的最大拉力为9N,问: 水平传送带足够长,传送带的上表面始终向右匀速运动,长为1米的薄木板A的正中央放置一个小木块B,A和B之间的动摩擦因数为0.2,A和传送带之间的动摩擦因数为0.5,B和传送带之间的动摩擦因数为0.4,薄木板的质量是木块质量的2倍,轻轻把AB整体放置在传送带的中央,传送带的上表面始终绷紧并处于水平状态,g取10m/s2,在刚放上很短的时间内,A、B的加速度大小分别为:( )
水平传送带足够长,传送带的上表面始终向右匀速运动,长为1米的薄木板A的正中央放置一个小木块B,A和B之间的动摩擦因数为0.2,A和传送带之间的动摩擦因数为0.5,B和传送带之间的动摩擦因数为0.4,薄木板的质量是木块质量的2倍,轻轻把AB整体放置在传送带的中央,传送带的上表面始终绷紧并处于水平状态,g取10m/s2,在刚放上很短的时间内,A、B的加速度大小分别为:( ) 。在把小物块从木板右端拉下去的过程中,求:
。在把小物块从木板右端拉下去的过程中,求: