题目内容
如图所示,在光滑、平直的轨道上静止着两辆完全相同的平板车,人从a车跳上b车,又立即从b车跳回a车,并与a车保持相对静止,此后a车的速率-b车的速率______(选‘大于”、“小于”或‘等于,’);在这个过程中,a车对人的冲量-右车对人的冲量______(选填“大于”、“小于,或.‘等于,).
【答案】分析:人与a、b组成的系统水平方向不受外力,水平方向动量守恒,由动量守恒定律分析两车速率关系.
解答:解:人与a、b组成的系统水平方向不受外力,水平方向动量守恒,则有
0=(m人+ma)va-mbvb
得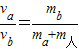 <1,则a车的速率小于b车的速率.
<1,则a车的速率小于b车的速率.
人对a车的冲量:Pa=△mava=mava;Pb=△mbvb=mbvb=(ma+m人)va>mava所以a车对人的冲量小于b车对人的冲量.
故答案为:小于;小于
点评:本题运用动量守恒定律分析两车速度关系,这个结果与人跳跃多少次没有关系,只要人最后落在a车上,a车的速率就小于b车的速率.
解答:解:人与a、b组成的系统水平方向不受外力,水平方向动量守恒,则有
0=(m人+ma)va-mbvb
得
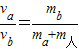 <1,则a车的速率小于b车的速率.
<1,则a车的速率小于b车的速率.人对a车的冲量:Pa=△mava=mava;Pb=△mbvb=mbvb=(ma+m人)va>mava所以a车对人的冲量小于b车对人的冲量.
故答案为:小于;小于
点评:本题运用动量守恒定律分析两车速度关系,这个结果与人跳跃多少次没有关系,只要人最后落在a车上,a车的速率就小于b车的速率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的
平面上有一个长为L的木板B,上表面粗糙.在其左端有一个光滑的 如图所示,在光滑的平台上,有一质量为m的物体,物体与轻绳的一端相连,轻绳跨过定滑轮(定滑轮的质量和摩擦不计)另一端被滑轮正下方站在地面上的人拉住,人与绳的接触点和定滑轮的高度差为h,若此人以速度v0 向右匀速前进s,求在此过程中人的拉力对物体所做的功.
如图所示,在光滑的平台上,有一质量为m的物体,物体与轻绳的一端相连,轻绳跨过定滑轮(定滑轮的质量和摩擦不计)另一端被滑轮正下方站在地面上的人拉住,人与绳的接触点和定滑轮的高度差为h,若此人以速度v0 向右匀速前进s,求在此过程中人的拉力对物体所做的功.