Question

【题目】如图所示，遥远的太空中有一孤立星体，半径为，质量为，分布均匀．有一空间站在距球心的圆轨道上做无动力飞行．现考虑从空间站向星体发射飞船，需要讨论飞船的着陆问题

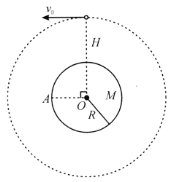
（1）人们提出了两种着陆方案，方案一：飞船相对空间站发射时速度指向球心，大小为．方案二：飞船发射时相对空间站速度指向空间站运动的反方向，大小为，请分别求出与的大小

（2）当空间站运动到图示位置时发射飞船，为使飞船能精确着陆在图中的点，试求飞船发射时的相对空间站的速度．（以上问题均不考虑空间站的反冲作用，且飞船总是沿切线方向着陆，飞船总是采取节省燃料的发射方式）

Answer 1

【答案】（1）所以，，（2）相对速度的方向指向球心，大小为

【解析】

（1）设空间站质量为，飞行速度为．

由牛顿第二定律得，所以，．

对于方案一，由角动量守恒得飞船着陆前瞬间的速度．

由机械能守恒得，

所以，．

对于方案二，由得，

所以，．

（2）如图所示，以为极轴建立极坐标．

设飞船的轨迹方程为．

当时，有．

当时，有．

所以，，所以，

所以，，

所以，时，，

所以， ， ①

．

设飞船发射时绝对速度为，相对速度为，着陆时速度为．

由角动量守恒有． ②

由机械能守恒有． ③

联立①②③得，

由此得，，

所以，相对速度的方向指向球心，大小为，与（1）中的方案一相同．