题目内容
如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( )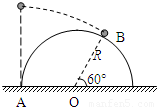
A.
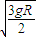
B.
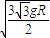
C.
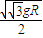
D.
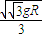
【答案】分析:根据平抛运动速度与水平方向夹角的正切值等于位移与水平方向夹角正切值的2倍,求出竖直方向上的位移,从而求出竖直方向上的分速度,根据速度方向求出平抛运动的初速度.
解答:解:飞行过程中恰好与半圆轨道相切于B点,知速度与水平方向的夹角为30°,设位移与水平方向的夹角为θ,则tanθ=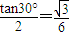 .
.
因为tanθ=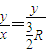 ,则竖直位移y=
,则竖直位移y=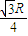 .
.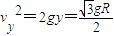 .
.
所以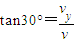 ,
,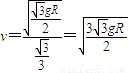 .故B正确,A、C、D错误.
.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,抓住速度方向,结合位移关系、速度关系进行求解.
解答:解:飞行过程中恰好与半圆轨道相切于B点,知速度与水平方向的夹角为30°,设位移与水平方向的夹角为θ,则tanθ=
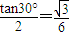 .
.因为tanθ=
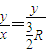 ,则竖直位移y=
,则竖直位移y=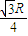 .
.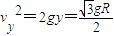 .
.所以
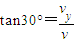 ,
,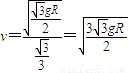 .故B正确,A、C、D错误.
.故B正确,A、C、D错误.故选B.
点评:解决本题的关键掌握平抛运动在水平方向和竖直方向上的运动规律,抓住速度方向,结合位移关系、速度关系进行求解.

练习册系列答案
相关题目
 (2013?徐汇区二模)如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( )
(2013?徐汇区二模)如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( ) 如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( )
如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则小球抛出时的初速度为( )
 B.
B.
 D.
D.

 B.
B. C.
C. D.
D.
