题目内容
如图所示，质量M=20kg的空箱子，放在光滑水平面上，箱子中有一个质量m=30kg的铁块，铁块与箱子的左端ab壁相距s=1m，它一旦与ab壁接触后就不会分开，铁块与箱底间的摩擦可以忽略不计．用水平向右的恒力F=10N作用于箱子，2s末立即撤去作用力，最后箱子与铁块的共同速度大小是（ ）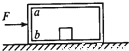
A．
m/sB．
m/sC．
m/sD．
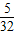m/s
【答案】分析：箱子受到恒力的作用做匀加速运动，使用牛顿运动定律求出2s末箱子的速度和位移，在用动量守恒定律列方程求解共同的速度．
解答：解：恒力F作用于箱子上时，箱子的加速度：
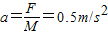
2s末，箱子的速度大小为：v=at=1m/s
箱子的位移：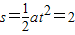
m
此时箱子刚好与铁块相碰，设碰后共同速度为v，根据动量守恒定律得：Mv=（M+m）v
联立以上各式可得：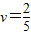
m/s
所以选项A正确，其他选项错误．
故选：A
点评：该题将牛顿运动定律与动量守恒定律结合，但情景相对简单，属于中档题目．
解答：解：恒力F作用于箱子上时，箱子的加速度：
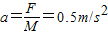
2s末，箱子的速度大小为：v=at=1m/s
箱子的位移：
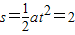m此时箱子刚好与铁块相碰，设碰后共同速度为v，根据动量守恒定律得：Mv=（M+m）v
联立以上各式可得：
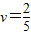m/s所以选项A正确，其他选项错误．
故选：A
点评：该题将牛顿运动定律与动量守恒定律结合，但情景相对简单，属于中档题目．
练习册系列答案
阅读快车系列答案
相关题目
（2013?荆州模拟）如图所示，质量m=2.2kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
如图所示，质量m=2.0kg的木块静止在水平面上，用大小F=20N、方向与水平方向成θ=37°角的力拉动木块，当木块运动到x=10m时撤去力F．不计空气阻力．已知木块与水平面间的动摩擦因数?=0.2，sin37°=0.6，cos37°=0.8．g取10m/s2．求：
如图所示，质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面，两桥面的圆弧半径均为20m．由于轮胎太旧，如果受到超过3×105N的压力时就会出现爆胎，则：
如图所示，质量m=2.0kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（2013?海淀区一模）如图所示，质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中．取g=10m/s2．