Question

【题目】如图所示，P、M为一截面为等腰梯形的透明棱镜ABCD的两条棱边的中点，AB=BC=AD=2l，校镜底角∠ADC=60°，EF为平行于CD的光屏，两束相同单色光同时垂直CD分别从P、M竖直射入棱镜，已知从P点射人的光从CD边射出时与CD的夹角为30°，且光屏上只有一个点(不考虑光在界面的反射)，c为单色光在真空中的传播速度，求：

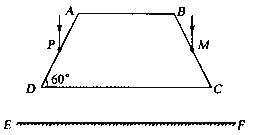
(ⅰ)该单色光在棱镜中的折射率n及从P点射人的光在棱镜中传播的时间；

(ii)光屏EF到CD边的距离.

Answer 1

【答案】(1) ， (2)

【解析】

因为射出光线与CD边夹角为，则从CD边射出光线的折射角为，由对称性可知，光线第一次的折射角与第二次的入射角相等，由折射定律可得折射率，根据求出从P点射人的光在棱镜中传播的时间；光屏上只有一个点，即从P、M两点射入的两束在EF上重合，设光屏EF到CD的距离为，由几何关系可得光屏EF到CD边的距离。

解：(1)因为射出光线与CD边夹角为，则从CD边射出光线的折射角为，由对称性可知，光线第一次的折射角与第二次的入射角相等，即折射角

由折射定律可得：

从P点射入的单色光在棱镜中传播的时间为：

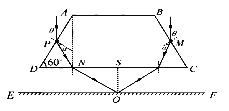
(2)光屏上只有一个点，即从P、M两点射入的两束在EF上重合，设光屏EF到CD的距离为，由几何关系可得：