Question

A、B两辆汽车在笔直的公路上同向行驶。当B车在A车前84m处时，B车速度为4m/s，且正以2m/s²的加速度做匀加速运动；经过一段时间后，B车加速度突然变为零。A车一直以20m/s的速度做匀速运动。经过12s后两车相遇。问B车加速行驶的时间是多少？

 

 

Answer 1

【答案】

6 s

【解析】设A车的速度为v_A，B车加速行驶时间为t，两车在t₀时相遇。则有

 s_A=v_At₀                        （2分）

 s_B=v_Bt +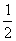at²+(v_B+at)(t₀-t)          （4分）

 式中，t₀＝12 s，S_A、S_B分别为A、B两车相遇前行驶的路程。依题意有s_A= s_B +s  （2分）

 代入数据 s=84 m  ,

解得       t₂=18 s不合题意。因此，B车加速行驶的时间为6 s。     （3分）