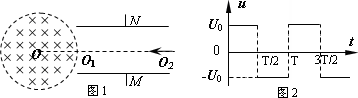题目内容
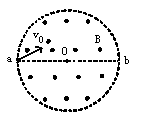
在真空中,半径为r=3×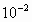 m的圆形区域内,有一匀强磁场,磁场的磁感应强度为B=0.2T,方向如图所示,一带正电粒子,以初速度
m的圆形区域内,有一匀强磁场,磁场的磁感应强度为B=0.2T,方向如图所示,一带正电粒子,以初速度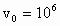 m/s的速度从磁场边界上直径ab一端a点处射入磁场,已知该粒子比荷q/m=
m/s的速度从磁场边界上直径ab一端a点处射入磁场,已知该粒子比荷q/m=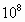 C/kg,不计粒子重力,则
C/kg,不计粒子重力,则
(1)粒子在磁场中做匀速圆周运动的半径是多少?
(2)若要使粒子飞离磁场时有最大的偏转角,其入射时粒子的方向应如何(以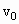 与Oa的夹角θ表示)?最大偏转角多大?
与Oa的夹角θ表示)?最大偏转角多大?
答案:
解析:
解析:
|
解:(1)粒子在磁场中受到的洛伦兹力F=Bq
r=
(2)假设粒子从c点飞出磁场,由(1)中可知粒子做圆周运动半径为r=
cosβ= 由于β<
θ= 最大偏转角
α= |

练习册系列答案
相关题目
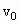 ,根据圆周运动规律F=
,根据圆周运动规律F=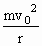 ,得:粒子做匀速圆周运动半径
,得:粒子做匀速圆周运动半径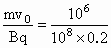 m=0.05m;
m=0.05m;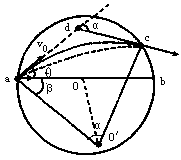
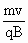 ,对于这一速度的粒子r为定值0.05m.设粒子圆周运动的圆心为
,对于这一速度的粒子r为定值0.05m.设粒子圆周运动的圆心为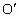 ,偏转角α等于
,偏转角α等于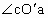 ,由于在
,由于在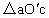 中,
中,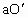 ,
,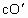 为定值,所以当
为定值,所以当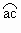 距离最大时
距离最大时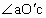 有最大值,故当ac与ab重合时偏转角最大,此时,
有最大值,故当ac与ab重合时偏转角最大,此时,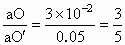 ,
,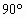 ,所以β=
,所以β=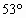 ,故入射时粒子的方向角
,故入射时粒子的方向角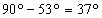 ,
,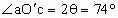 .
.