题目内容
在水平面上放着两个质量分别为2kg和3kg的小铁块m和M，它们之间用一原长为10cm，劲度系数为100N/m的轻弹簧相连，铁块与水平面之间的动摩擦因数均为0.2．铁块M受到一大小为20N的恒定水平外力F，两个铁块一起向右做匀加速直线运动，如图所示．这时两铁块之间弹簧的长度应为（重力加速度g取10m/s2）（ ）分析：对整体受力分析，由牛顿第二定律可求得系统加速度；再对m分析可求得弹簧的拉力；再由胡克定律可求得弹簧的伸长量．
解答：解：整体水平方向受拉力、摩擦力；由牛顿第二定律可知：
F-μ（M+m）g=（M+m）a
解得：a=
=
=2m/s2；
m受拉力和摩擦力而做匀加速直线运动：
拉力F′=ma+μmg=2×2+0.2×20N=8N；
由胡克定律可知，形变量x=
=0.08m
则弹簧的长度为l+x=0.18m=18cm；
故选D．
F-μ（M+m）g=（M+m）a
解得：a=
| F-μ(m+M) |
| (m+M) |
| 20-0.2(20+30) |
| (2+3) |
m受拉力和摩擦力而做匀加速直线运动：
拉力F′=ma+μmg=2×2+0.2×20N=8N；
由胡克定律可知，形变量x=
| F′ |
| K |
则弹簧的长度为l+x=0.18m=18cm；
故选D．
点评：本题关键在于先以整体为研究对象，再用隔离法进行分析，注意整体法时不能分析内力．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
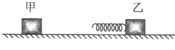如图所示，在光滑水平面上放着质量均为 m=lkg的两个物块，开始物块乙静止，在乙上系有一个轻质弹簧．物块甲以速度v=lOm/s向乙运动．当甲与轻质弹簧接触后粘连在一起，继续在水平面上运动（弹簧始终在弹性限度内）．在运动过程中，求：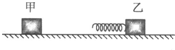
时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。
= 
（2）
。
。）
= m1
+ m2
+ m3
+ … + mn
只能是系统外力的矢量和，等式右边也是矢量相加。
x 。
Mg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。
Mg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 
〔x -〈L-l〉〕。
。
= m2a
g
。
= m1
+ m2
+ m3
+ … + mn
，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：
g 。
。
求a1 。
。
at2 ②
a1xt2 ③
+ 
* = m 
（注：
*为惯性力），此题极简单。过程如下——
a相 t2 （3）