题目内容
如图所示，穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连，手拉细线的另一端，让小球在水平面上以角速度ω1沿半径为a的圆周做匀速圆周运动．所有摩擦力均不考虑．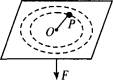
(1)这时细线上的张力多大?
(2)若突然松开手中的细线，经时间△t再握紧细线，随后小球沿半径为b的圆周做匀速圆周运动．试问：△t等于多大?这时的角速度ω2为多大?
答案：
解析：
提示：
解析：
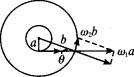
(1)F＝maω12(2)△t＝  提示：(1)绳上拉力就等于小球做圆周运动的向心力，故F＝maω12．
(2)突然松开手，则绳对小球的拉力立即消失，小球将沿切线方向飞出做匀速直线运动．如图所示，小球通过的位移为△s＝
当小球运动到外圆周上瞬间，其速度大小不变，仍为ω1a，由于绳子的瞬间收缩使小球的速度发生突变——沿半径方向的速度消失，沿切线方向的速度大小不变． 即有
|
，从而运动的时间为△t＝△s/v＝
＝sin
=
，解之得ω2＝
ω1．提示：
练习册系列答案
阳光课堂同步练习系列答案
相关题目
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别挂上小球C和物体B，在B的下端再挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时圆周运动的半径为R，现剪断连接A、B的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，一根不可伸长的轻绳穿过小孔．绳的两端分别拴有一小球C和一质量为m的物体B，在物体B的下端还悬挂有一质量为3m的物体A．使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动的半径为R．现剪断连接A、B的绳子，稳定后，小球以2R的半径在水平面上做匀速圆周运动，则下列说法正确的（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别栓上一小球C和一物体B，在B的下端再悬挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动半径为R．现剪断连接AB的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
