题目内容
如图所示,倾角为θ=45°的光滑斜轨与半径为R的光滑半圆环相切,切点为B.一质量为m的小球从斜轨上高为h=2R的A处无初速下滑进入圆环轨道.
(1)小球将能到达圆环轨道上多高的地方?小球脱离圆环轨道时的速度多大?
(2)若小球从斜轨上高为h=5R/2处滑下,进入圆环轨道,接着小球从圆环最高点C水平飞出,又落到斜轨上.在小球击中斜轨前的瞬间,小球的速度多大?
解:(1)小球脱离圆环时,对圆环的压力为零.设小球的速度为v,DO和CO间的角度为α.

mgcosα=m![]()
以最低点为重力势能的零点mg2R=mgR(1+cosα)+![]() mv2
mv2
cosα=![]()
小球能到达的高度为h=R(1+cosα)=![]() R.
R.
(2)小球从A到C,机械能守恒,有![]() mvC2+mg·2R=mgh=mg·
mvC2+mg·2R=mgh=mg·![]() R
R
解得vC=![]()
如图建立坐标系,设小球落在斜轨上的坐标是P(x,y)

小球的轨迹方程为y=![]() ①
①
AB斜轨的方程为y=-xtan45°+(![]() +1)R ②
+1)R ②
将vC=![]() 代入①,得y=
代入①,得y=![]() ③
③
y=-x+(![]() +1)R ④
+1)R ④
解③④得x=![]() R,y=R(另一组解不适合,舍去)
R,y=R(另一组解不适合,舍去)
从C到落点,机械能守恒,
![]() mvc2+mgy=
mvc2+mgy=![]() mv2,解得v=
mv2,解得v=![]() .
.

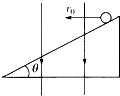 如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问:
如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问: 如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( )
如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( ) (2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )
(2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )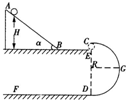 如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的
如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的