题目内容
如图所示，质量均为m的两物体A．B分别与轻质弹簧的两端 相连接，将它们静止放在地面上。一质量也为m的小物体C从距A物高处由静止开始下落。C与A相碰后立即粘在一起向下运动，以后不再分开。当A与C运动到最高点时，物体B对地面刚好无压力。不计空气阻力。弹簧始终处于弹性限度内。已知重力加速度为g。求：
（1）A与C一起开始向下运动时的速度大小；
（2）A与C一起运动的最大加速度大小；
（3）弹簧的劲度系数。
（1）设小物体C从静止开始运动到A点时速度为
，由机械能守恒定律
……………………（2分）
设C与A碰撞粘在一起时速度为
，由动量守恒定律
……………………（3分）
求出 
……………………（1分）
（2） A与C一起将在竖直方向作简谐运动。当A与C运动
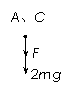
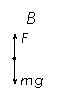到最高点时，回复力最大，加速度最大。
A．C受力图，B受力图如右图 …………………（2分）
B受力平衡有 F = mg ……………………（2分）
对A．C应用牛顿第二定律
F + 2mg = 2ma ……………………（2分）
求出 a = 1．5g ……………………（2分）
（3） 设弹簧的劲度系数为k
开始时A处于平衡状态，设弹簧的压缩形变量为△x
对A有 
………（1分）
当A与C运动到最高时，设弹簧的拉伸形变量为△x′
对B有 
………（1分）
由以上两式得 
………（1分）
因此，在这两个位置时弹簧的弹性势能相等：E弹＝E弹′
对A．C，从原平衡位置到最高点，根据机械能守恒定律
E弹＋
＋ E弹′ ………（3分）
解得 
……… （2分）
口算题卡北京妇女儿童出版社系列答案
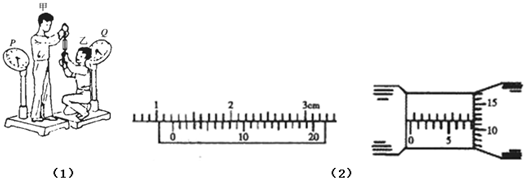
（2011?河西区二模）如图所示，质量均为m的A、B两球之间系着一根不计质量的弹簧，放在光滑的水平面上，A球紧靠竖直墙壁，今用水平力F将B球向左推压弹簧，平衡后，突然将F撤去，在这瞬间（ ）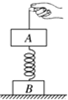 
如图所示，质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连，开始时B放在地面上，A、B均处于静止状态，现通过细绳将A缓慢地向上拉起，当B刚要离开地面时，求A上升距离（假设弹簧一直在弹性限度内，重力加速度g已知）
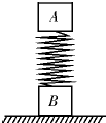（2013?湖南模拟）如图所示，质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端，当A静止时弹簧的压缩量为l．现用一竖直向下的恒力F=3mg作用于A上，当A运动一段距离x，后撤去F，结果B刚好不离开水平面，则l：x的值为（ ）