题目内容
水平放置、足够长的光滑平行金属导轨MN和PQ相距d=0.4m,接在MP之间的定值电阻R=0.9Ω;质量M=80g、电阻R=0.3Ω的金属棒ab静止在金属导轨上,导轨与金属棒间的动摩擦因素为μ=0.2(视最大静摩擦力等于滑动摩擦力).ac、cd和db三段的长度相同、电阻值相等,金属棒与导轨接触良好;导轨和连线的电阻不计,整个装置处在垂直于轨道平面向下的匀强磁场中,俯视如图.开始时,金属棒距MP距离为L=0.2m,磁感应强度B=1T,磁感应强度每秒增加0.2T.(1)求经过多长时间金属棒开始运动.
(2)若保持B=2T不变,给金属棒施加一个水平向右且垂直于棒的力,让金属棒以10m/s的速度匀速向右运动,求金属棒两端的电势差Uab.

【答案】分析:(1)磁感应强度均匀增加时,回路中产生恒定电流,导体所受的安培力均匀增大,当安培力大小等于导体所受的最大静摩擦力时,金属棒开始运动.由法拉第电磁感应定律求解感应电动势,由欧姆定律求解感应电流,由平衡条件求出时间.
(2)若保持B=2T不变,金属棒以10m/s的速度匀速向右运动,由E=Bdv求出感应电动势.金属棒两端的电势差Uab等于cd间的电势差和导轨之外ac、da所产生的感应电动势之和.
解答:解:(1)感应电动势为:E=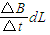 =0.2×0.4×0.2=0.016V
=0.2×0.4×0.2=0.016V
感应电流:I=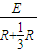 =
=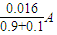 =0.016A
=0.016A
开始运动:(B+t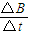 )Id=μmg
)Id=μmg
代入解得:t=120s
(2)金属棒上各段产生的感应电动势为:Eac=Ecd=Edb=Bdv=2×0.4×10=8V
回路中,Ucd=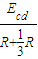 =7.2V
=7.2V
开路部分:Uac=Udb=Eac=Edb=8V
则a、b间电势差为Uab=Uac+Ucd+Udb=23.2V
答:
(1)经过120s时间金属棒开始运动.
(2)金属棒两端的电势差Uab是23.2V.
点评:本题中第1题是感生电动势问题,由法拉第定律求解感应电动势,第2题是动生电动势问题,由E=BLv求出电动势,注意金属棒三段都要产生感应电动势.
(2)若保持B=2T不变,金属棒以10m/s的速度匀速向右运动,由E=Bdv求出感应电动势.金属棒两端的电势差Uab等于cd间的电势差和导轨之外ac、da所产生的感应电动势之和.
解答:解:(1)感应电动势为:E=
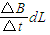 =0.2×0.4×0.2=0.016V
=0.2×0.4×0.2=0.016V 感应电流:I=
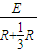 =
=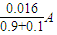 =0.016A
=0.016A 开始运动:(B+t
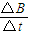 )Id=μmg
)Id=μmg 代入解得:t=120s
(2)金属棒上各段产生的感应电动势为:Eac=Ecd=Edb=Bdv=2×0.4×10=8V
回路中,Ucd=
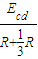 =7.2V
=7.2V 开路部分:Uac=Udb=Eac=Edb=8V
则a、b间电势差为Uab=Uac+Ucd+Udb=23.2V
答:
(1)经过120s时间金属棒开始运动.
(2)金属棒两端的电势差Uab是23.2V.
点评:本题中第1题是感生电动势问题,由法拉第定律求解感应电动势,第2题是动生电动势问题,由E=BLv求出电动势,注意金属棒三段都要产生感应电动势.

练习册系列答案
相关题目
 如图所示,一矩形轻质柔软反射膜可绕过O点垂直纸面的水平轴转动,其在纸面上的长度为L1,垂直纸面的长度为L2.在膜的下端(图中A处)挂有一平行于转轴,质量为m,长为L3的导体棒使膜形成平面.在膜下方水平放置一足够大的太阳能光电池板,能接收到经反射膜反射到光电池板上的所有光能,并将其转化成电能.光电池板可等效为一个电池,输出电压恒定为U;输出电流正比于光电池板接收到的光能(设垂直于入射光单位面积上的光功率保持恒定).导体棒处在方向竖直向上的匀强磁场B中,并与光电池构成回路,流经导体棒的电流垂直纸面向外(注:光电池与导体棒直接相连,连接导线未画出).
如图所示,一矩形轻质柔软反射膜可绕过O点垂直纸面的水平轴转动,其在纸面上的长度为L1,垂直纸面的长度为L2.在膜的下端(图中A处)挂有一平行于转轴,质量为m,长为L3的导体棒使膜形成平面.在膜下方水平放置一足够大的太阳能光电池板,能接收到经反射膜反射到光电池板上的所有光能,并将其转化成电能.光电池板可等效为一个电池,输出电压恒定为U;输出电流正比于光电池板接收到的光能(设垂直于入射光单位面积上的光功率保持恒定).导体棒处在方向竖直向上的匀强磁场B中,并与光电池构成回路,流经导体棒的电流垂直纸面向外(注:光电池与导体棒直接相连,连接导线未画出).
 的透明液体。容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置。若容器高为2
的透明液体。容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置。若容器高为2 dm,底面半径为R=(1+
dm,底面半径为R=(1+  )dm,OM=1dm,在容器中央正上方1dm 处水平水平放置一足够长的刻度尺,求光源S发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)
)dm,OM=1dm,在容器中央正上方1dm 处水平水平放置一足够长的刻度尺,求光源S发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)
 的透明液体。容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置。若容器高为2dm,底面半径为R=(1+
的透明液体。容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置。若容器高为2dm,底面半径为R=(1+  )dm,OM=1dm,在容器中央正上方1dm
处水平水平放置一足够长的刻度尺,求光源S发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)
)dm,OM=1dm,在容器中央正上方1dm
处水平水平放置一足够长的刻度尺,求光源S发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)