��Ŀ����
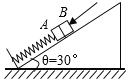
����Ŀ����ͼ��ʾ��һ�㹻���Ĺ̶��⻬б�����![]() =37���������A��B������
=37���������A��B������![]() =1kg��
=1kg��![]() =4kg�������֮���������L=0��5m�������ɳ��ܵ��������ΪT=12N����Bʩ��һ��б�����ϵ��� F��ʹA��B�ɾ�ֹ��ʼһ�������˶�����F������ gȡ10m/s2��sin37��=0��6��cos37��=0��8����
=4kg�������֮���������L=0��5m�������ɳ��ܵ��������ΪT=12N����Bʩ��һ��б�����ϵ��� F��ʹA��B�ɾ�ֹ��ʼһ�������˶�����F������ gȡ10m/s2��sin37��=0��6��cos37��=0��8����
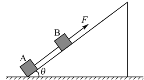
(1)��ijһʱ�����������ϣ����ʱ����F�Ĵ�С��
(2)����������˲��A��B���ٶ�Ϊ3m/s�����Ϻ�����F���䣬��A�˶�����ߵ�ʱ��A��B֮��ľ��롣
���𰸡���1��![]() ����2��
����2��![]()
��������
��1����ijһʱ�����������ϣ���ʱT=12N����A��B�������������ţ�ٵڶ����ɵã�
F����mA+mB��gsin��=��mA+mB��a
��A���壺T��mAgsin��=mAa
�������ݽ�ã�F=60N
��2������б������Ϊ������A���壺��mAgsin��=mAaA����ã�aA=-6m/![]() .
.
��Ϊv0=3m/s������A���嵽��ߵ�ʱ��Ϊ��t=![]() =
=![]() s=0.5s
s=0.5s
�˹���A�����λ��Ϊ��xA=![]() t=0.75m
t=0.75m
��B���壺F��mBgsin��=mBaB�����aB=9m/![]()
xB=v0t+![]() aB
aB![]() =��3
=��3![]() 0.5+
0.5+![]() 9
9![]() ��m=2.625m
��m=2.625m
�������������x=xB��xA+L
�������ݽ�ã���x=2.375m

��ϰ��ϵ�д�
�����Ŀ