题目内容
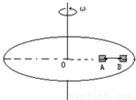
如图所示，在匀速转动的圆盘上，沿半径方向放置以细线相连的质量均为m的A、B两个小物块，A离轴心r1=20cm，B离轴心r2=30cm，A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍．求：（1）当细线上出现张力时，圆盘转动的角速度ω=？
（2）欲使A、B与盘面间不发生相对滑动，则盘转动的最大角速度多大？（g=10m/s2）
【答案】分析：（1）由题意可知当细线上出现张力时，B与盘间已达的最大静摩擦力，故静摩擦力充当向心力，由向心力公式可求得角速度；
（2）当A恰好开始滑动时，说明A已达到最大静摩擦力，由向心力公式可求得角速度，此角速度为最大角速度；
解答：解：（1）当细线上开始出现张力时，B与圆盘之间的静摩擦力达到最大值．
对B：kmg=mω2rB
即ω=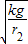
=
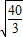rad/s
（2）当A开始滑动时，A、B所受静摩擦力均达最大，设此时细绳张力为T：
对B：FT+μmg=mω2RB
对A：μmg-FT=mω2RA
联立解得：ω=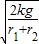
=4rad/s
答：（1）当细线上出现张力时，圆盘转动的角速度为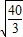
rad/s；
（2）欲使A、B与盘面间不发生相对滑动，则盘转动的最大角速度为4rad/s．
点评：本题考查圆周运动中力与运动的关系，注意本题中为静摩擦力与绳子的拉力充当向心力，故应注意静摩擦力是否已达到最大静摩擦力．
（2）当A恰好开始滑动时，说明A已达到最大静摩擦力，由向心力公式可求得角速度，此角速度为最大角速度；
解答：解：（1）当细线上开始出现张力时，B与圆盘之间的静摩擦力达到最大值．
对B：kmg=mω2rB
即ω=
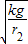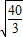=rad/s （2）当A开始滑动时，A、B所受静摩擦力均达最大，设此时细绳张力为T：
对B：FT+μmg=mω2RB
对A：μmg-FT=mω2RA
联立解得：ω=
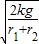=4rad/s答：（1）当细线上出现张力时，圆盘转动的角速度为
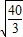rad/s；（2）欲使A、B与盘面间不发生相对滑动，则盘转动的最大角速度为4rad/s．
点评：本题考查圆周运动中力与运动的关系，注意本题中为静摩擦力与绳子的拉力充当向心力，故应注意静摩擦力是否已达到最大静摩擦力．
练习册系列答案
相关题目
如图所示，在匀速转动的水平圆盘上，沿半径方向放着用细线相连的质量相等的两个物体A和B，它们与盘间的摩擦因数相同，当圆盘转动到两个物体刚好还未发生滑动时，烧断细线，两个物体的运动情况是（ ）
如图所示，在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动，物体相对桶壁静止则（ ）
如图所示，在匀速转动的水平圆盘上，在离转轴某一距离处放一滑块，该滑块恰能跟随圆盘做匀速圆周运动而不产生相对滑动，则下列情况中，仍然能使滑块与圆盘保持相对静止的是（ ）
如图所示，在匀速转动的水平圆盘上，沿半径方向放着用细线相连的质量相等的两个物体A和B，它们与盘间的摩擦因数相同，当圆盘转动到两个物体刚好还未发生滑动时，烧断细线，则（ ）
如图所示，在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动，物体相对筒壁静止，则（ ）| A、物体受到3个力的作用 | B、物体所受向心力是物体所受的重力提供的 | C、物体所受向心力是物体所受的弹力提供的 | D、物体所受向心力是物体所受的静摩擦力提供的 |