题目内容
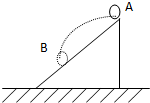
从倾角为θ的斜面顶端用弹簧枪把一个原来静止的小球以15J的初动能水平弹射出去,小球刚好能落到斜面的底端.已知小球落到斜面底端时动能为35J.不计空气阻力,小球在飞行过程中,重力对小球做功为 J,斜面的倾角θ为 .
【答案】分析:对小球的平抛运动过程运用动能定理列式可以求解出合力做的功,等于重力做的功;斜面的倾斜角即为位移与水平方向的夹角,根据动能的表达式求出初末速度之比,再根据平抛运动的位移偏转角θ正切与速度偏转角α的正切的关系公式tanθ=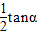 求解位移方向与水平方向的夹角.
求解位移方向与水平方向的夹角.
解答:解:小球的平抛运动过程中只有重力做功,运用动能定理,有
W=Ek2-Ek1=35J-15J=20J
即重力做功为20J;
小球初末速度的比值为: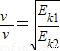 =
=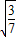
故小球的末速度的竖直分量与水平分量之比为:tanα=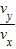 =
=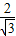
小球的位移与水平方向夹角θ的正切为:tanθ=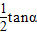 =
=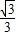 ,故θ=30°;
,故θ=30°;
故答案为:20,30°.
点评:本题关键根据动能定理求出重力做的功,然后根据动能表达式求出初末速度之比,进一步得到末速度的竖直分量与水平分量之比,即求出速度偏转角的正切值,然后根据平抛运动的位移偏转角的正切与速度偏转角的正切的关系公式tanθ=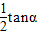 求解位移方向与水平方向的夹角.
求解位移方向与水平方向的夹角.
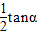 求解位移方向与水平方向的夹角.
求解位移方向与水平方向的夹角.解答:解:小球的平抛运动过程中只有重力做功,运用动能定理,有
W=Ek2-Ek1=35J-15J=20J
即重力做功为20J;
小球初末速度的比值为:
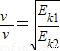 =
=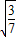
故小球的末速度的竖直分量与水平分量之比为:tanα=
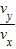 =
=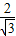
小球的位移与水平方向夹角θ的正切为:tanθ=
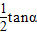 =
=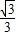 ,故θ=30°;
,故θ=30°;故答案为:20,30°.
点评:本题关键根据动能定理求出重力做的功,然后根据动能表达式求出初末速度之比,进一步得到末速度的竖直分量与水平分量之比,即求出速度偏转角的正切值,然后根据平抛运动的位移偏转角的正切与速度偏转角的正切的关系公式tanθ=
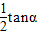 求解位移方向与水平方向的夹角.
求解位移方向与水平方向的夹角. 
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图所示,从倾角为θ=30°的斜面顶端以初动能E1=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E2为( )
如图所示,从倾角为θ=30°的斜面顶端以初动能E1=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E2为( )| A、8J | B、12J | C、14J | D、16J |
 如图所示,一物体从倾角为30°的斜面顶端由静止开始下滑,s1段光滑,s2段有摩擦,已知s2=2s1,物体到达底部的速度刚好为零,则s2段的动摩擦因数μ为多少?
如图所示,一物体从倾角为30°的斜面顶端由静止开始下滑,s1段光滑,s2段有摩擦,已知s2=2s1,物体到达底部的速度刚好为零,则s2段的动摩擦因数μ为多少?
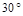 和
和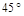 的斜面顶端抛出,如图所示,两斜面足够长,小球均落在斜面上。小球从抛出到第一次落到斜面上的过程中,两小球的位移大小之比为:( )
的斜面顶端抛出,如图所示,两斜面足够长,小球均落在斜面上。小球从抛出到第一次落到斜面上的过程中,两小球的位移大小之比为:( )
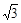 :3
:3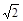 :3
:3