Question

【题目】如图所示，质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上，从A点随传送带运动到水平部分的最右端B点，经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道，恰能做圆周运动．C点在B点的正上方，D点为轨道的最低点．小物块离开D点后，做平抛运动，恰好垂直于倾斜挡板打在挡板跟水平面相交的E点．已知半圆轨道的半径R=0.9m，D点距水平面的高度h=0.75m，取g=10m/s2 ， 试求：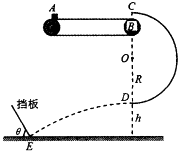

（1）摩擦力对物块做的功；
（2）小物块经过D点时对轨道压力的大小；
（3）倾斜挡板与水平面间的夹角θ．

Answer 1

【答案】
（1）

解：设小物块经过C点时的速度大小 ，因为经过C时恰好能完成圆周运动，由牛顿第二定律可得：

mg= ，解得 =3m/s

小物块由A到B过程中，设摩擦力对小物块做的功为W，由动能定理得：

W= ，解得W=4.5J

故摩擦力对物块做的功为4.5J

（2）

解：设小物块经过D点时的速度为 ，对由C点到D点的过程，由动能定理的：

mg.2R=

小物块经过D点时，设轨道对它的支持力大小为 ，由牛顿第二定律得：

﹣mg=

联立解得 =60N， =3 m/s

由牛顿第三定律可知，小物块对轨道的压力大小为：

= =60N．

故小物块经过D点时对轨道的压力大小为60N

（3）

解：小物块离开D点做平抛运动，设经时间t打在E点，由h= 得：t= s

设小物块打在E点时速度的水平、竖直分量分别为 、 ，速度跟竖直方向的夹角为α，则：

又tanα= =

联立解得α=60°

再由几何关系可得θ=α=60°

故倾斜挡板与水平面的夹角θ为60°

【解析】本题（1）的关键是明确小物块经过C点时恰好能做圆周运动的条件是重力等于向心力，然后再由动能定理即可求解；（2）题的关键是根据动能定理或机械能守恒定律求出小物块到达D点时的速度，然后再根据牛顿第二定律和牛顿第三定律即可求解；（3）题的关键是根据平抛运动规律并结合几何知识即可求出所求．
【考点精析】本题主要考查了平抛运动和向心力的相关知识点，需要掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动；向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力才能正确解答此题．