Question

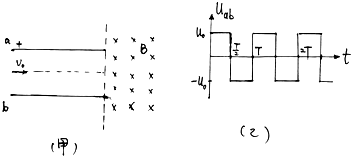
如图（甲）所示，两块平行金属板水平放置，间距d=0.1m，板长l=0.8m．一个可以看成质点的带正电微粒（重力不计），荷质比q/m=0.8（c/kg），以速度V₀=2m/s，从两板中间沿水平方向射入平行金属板，在两板之间加上如图（乙）的交变电压，U₀=1（V），T=0.04（s）．在平行金属板的右边有范围足够宽的垂直于纸面向里的匀强磁场，B=

π

24

×10³（T），设微粒在t=

1

8

T时刻水平向右进入电场．求：

（1）微粒在电场中运动经过第一个0.04（s）时间内，在竖直方向运动的距离d₀为多大？
（2）微粒第一次射出电场前，在竖直方向运动的最大距离d_m为多大？
（3）微粒最后从平行金属板左边射出时，距左边入射点的竖直距离为多少？

Answer 1

分析：微粒在

1

8

T时进入电场，先匀加速

1

8

T，然后匀减速运动

1

8

T，再反向匀加速…对照电场力方向分析出对应的运动情况，根据位移时间公式求出竖直方向运动的距离；
粒子水平方向匀速运动，由此求出运动时间，竖直方向做如第一问运动情况中的周期性运动，看运动时间内有多少个周期，算出对应的竖直位移；
求出粒子在磁场中圆周运动的周期，其在磁场中运动的时间恰好为交变电场的

3

4

T，从而判断出返回过程与前面过程为对称图形，然后结合几何知识求解．

解答：解：（1）前

3

8

T运动的距离为S₁
S₁=

1

2

qU0

md

（

3

8

T）²
第一个

1

8

T运动的距离S₂=

1

2

qU0

md

（

1

8

T）²
所以d=2（S₁-S₂）=

2

16

qU0T2

md

=1.6mm
（2）因为d_m=10d₀+2s₂=16mm+0.2mm=16.2mm
（3）在磁场中运动的周期T′=

2πm

qB

=6×10^-2s
半周时间t=3×10^-2s=

3

4

T
r=

mv0

qB

=

60

π

×10^-3m
返回过程与前面过程为对称图形．
所以d=2r-20d₀=

120

π

×10^-3-20×1.6×10^-3=6.2×10^-3m
答：（1）微粒在电场中运动经过第一个0.04（s）时间内，在竖直方向运动的距离d₀为1.6mm．
（2）微粒第一次射出电场前，在竖直方向运动的最大距离d_m为16.2mm．
（3）微粒最后从平行金属板左边射出时，距左边入射点的竖直距离为6.2×10^-3m．

点评：解决本题的关键是将粒子在电场中的偏转运动情况与电场的交变周期对应起来．