题目内容
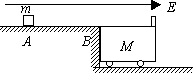
 如图所示,光滑绝缘平台上A点有质量为m=1kg的带电小物块,A、B间距离s=0.64m;质量为M=3kg、长为L=1m的不带电绝缘小车停在光滑水平地面上,且紧靠平台右侧,上表面与平台等高.此区间有E=2.5×103N/C的水平向右匀强电场,方向水平向右,t=0时刻小物块由静止开始向右运动,到达B处时撤去此电场,小物块由A至B过程中的动量满足条件Px=5.0
如图所示,光滑绝缘平台上A点有质量为m=1kg的带电小物块,A、B间距离s=0.64m;质量为M=3kg、长为L=1m的不带电绝缘小车停在光滑水平地面上,且紧靠平台右侧,上表面与平台等高.此区间有E=2.5×103N/C的水平向右匀强电场,方向水平向右,t=0时刻小物块由静止开始向右运动,到达B处时撤去此电场,小物块由A至B过程中的动量满足条件Px=5.0| Sx |
(1)小物块带电量q;
(2)小物块与小车间的动摩擦因数μ;
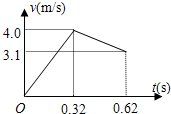
(3)在t=0时刻到碰撞前过程中,通过计算定量作出小物块相对地面的v-t图线(以向右方向为正).
分析:(1)根据题目中小物块由A至B过程中的动量满足条件与动量的定义,先求出小物块到达B点时的速度,然后使用动能定律求出小物块的带电量;
(2)小物块和小车处于光滑的水平面上,系统满足动量守恒定律,列出公式,求得二者共同的速度;小物块在小车上滑动的过程中,只有摩擦力做功,然后根据能量的转化与守恒,求出摩擦因数.
(3)对小物块进行受力分析,求得各段的加速度和各点的速度,然后画图.
(2)小物块和小车处于光滑的水平面上,系统满足动量守恒定律,列出公式,求得二者共同的速度;小物块在小车上滑动的过程中,只有摩擦力做功,然后根据能量的转化与守恒,求出摩擦因数.
(3)对小物块进行受力分析,求得各段的加速度和各点的速度,然后画图.
解答:解:(1)在B点:PB=5.0
=mVB
代入数据解得:VB=4.0m/s
由A→B据动能定理:EqS=
mv2
∴q=
=5.0×10-3C
(2)小物与小车相互作用至相对静止全过程,有:
系统动量守恒:mvB=(m+M)V共
∴V共=1.0m/s
系统能量守恒得:μmg?2L=
mv2-
(m+M)
代入数据解得:μ=0.3
(3)在A→B中,a1═12.5m/s2
得:t1=
=0.32s
在小物滑上小车至碰前过程,取向右为正:a'1=
=μg=3.0m/s2
a2=
=1.0m/s2
 L=(vBt2-
L=(vBt2-
a'1t22)-
a2t22代入数据整理得:
2t22-4t2+1=0
∴t2≈0.3s (另一根舍去)
由v'1=vB-a'1t2 得v'1=3.1m/s
画出v-t图象如下:
答:(1)小物块带电量为5.0×10-3C;
(2)小物块与小车间的动摩擦因数是0.3;
(3)在t=0时刻到碰撞前过程中,通过计算定量作出小物块相对地面的v-t图线如图.
| S |
代入数据解得:VB=4.0m/s
由A→B据动能定理:EqS=
| 1 |
| 2 |
∴q=
m
| ||
| 2ES |
(2)小物与小车相互作用至相对静止全过程,有:
系统动量守恒:mvB=(m+M)V共
∴V共=1.0m/s
系统能量守恒得:μmg?2L=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 共 |
代入数据解得:μ=0.3
(3)在A→B中,a1═12.5m/s2
得:t1=
| VB |
| a1 |
在小物滑上小车至碰前过程,取向右为正:a'1=
| μmg |
| m |
a2=
| μmg |
| M |
 L=(vBt2-
L=(vBt2-| 1 |
| 2 |
| 1 |
| 2 |
2t22-4t2+1=0
∴t2≈0.3s (另一根舍去)
由v'1=vB-a'1t2 得v'1=3.1m/s
画出v-t图象如下:
答:(1)小物块带电量为5.0×10-3C;
(2)小物块与小车间的动摩擦因数是0.3;
(3)在t=0时刻到碰撞前过程中,通过计算定量作出小物块相对地面的v-t图线如图.
点评:本题综合考查了动能定理、动量守恒定律以及能量守恒定律,综合性较强,对学生的能力要求较高,关键需理清运动过程,选择合适的规律进行求解.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
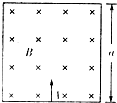 如图所示,光滑绝缘壁围成的正方形匀强磁场区域,边长为a磁场的方向垂直于正方形平面向里,磁感应强度的大小为B.有一个质量为m、电量为q的带正电的粒子,从下边界正中央的A孔垂直于下边界射入磁场中.设粒子与绝缘壁碰撞时无能量和电量损失,不计重力和碰撞时间.
如图所示,光滑绝缘壁围成的正方形匀强磁场区域,边长为a磁场的方向垂直于正方形平面向里,磁感应强度的大小为B.有一个质量为m、电量为q的带正电的粒子,从下边界正中央的A孔垂直于下边界射入磁场中.设粒子与绝缘壁碰撞时无能量和电量损失,不计重力和碰撞时间.