题目内容
 如图所示,两平行金属板P1和P2之间的电压为U.一个带负电的粒子在两板间沿虚线所示路径做加速直线运动. 粒子通过两平行板后从O点进入另一磁感应强度为B的匀强磁场中,在洛伦兹力的作用下,粒子做匀速圆周运动,经过半个圆周后打在挡板MN上的A点. 已知粒子的质量为m,电荷量为q. 不计粒子重力. 求:
如图所示,两平行金属板P1和P2之间的电压为U.一个带负电的粒子在两板间沿虚线所示路径做加速直线运动. 粒子通过两平行板后从O点进入另一磁感应强度为B的匀强磁场中,在洛伦兹力的作用下,粒子做匀速圆周运动,经过半个圆周后打在挡板MN上的A点. 已知粒子的质量为m,电荷量为q. 不计粒子重力. 求:(1)粒子进入磁场时的速度v;
(2)O、A两点间的距离x.
分析:(1)带电粒子在加速电场中电场力做功等于粒子动能的增加量,由动能定理 可以求得粒子进入磁场时的速度v;
(2)带电粒子在磁场中做匀速圆周运动,在磁场中运动半个圆周后打在A点,洛伦兹力提供向心力;O、A两点间的距离是圆的直径.
(2)带电粒子在磁场中做匀速圆周运动,在磁场中运动半个圆周后打在A点,洛伦兹力提供向心力;O、A两点间的距离是圆的直径.
解答:解:(1)带电粒子在加速电场中电场力做功等于粒子动能的增加量,由动能定理 qU=
mv2得:
v=
(2)设带电粒子的轨道半径为R,洛伦兹力提供向心力,得:
qvB=m
整理得:
R=
O、A两点间的距离x:x=2R=
=
?
答:(1)粒子进入磁场时的速度v=
;
(2)O、A两点间的距离为
?
.
| 1 |
| 2 |
v=
|
(2)设带电粒子的轨道半径为R,洛伦兹力提供向心力,得:
qvB=m
| v2 |
| R |
整理得:
R=
| mv |
| qB |
O、A两点间的距离x:x=2R=
| 2mv |
| qB |
| 2 |
| B |
|
答:(1)粒子进入磁场时的速度v=
|
(2)O、A两点间的距离为
| 2 |
| B |
|
点评:该题中带电粒子先在电场中加速,后在匀强磁场中做匀速圆周运动,都是基本的情景.题目简单.

练习册系列答案
相关题目
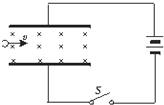 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )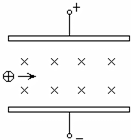 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=