题目内容
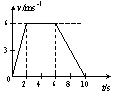
图表示一个质量为2kg的重物在竖直悬线的拉力作用下沿竖直方向向上运动的速度-时间图象。从图象可知,在________时间内,悬线的拉力最大,为________N;在________时间内,悬线的拉力最小,为________N。(g取10m/s2)
答案:
解析:
解析:
|
0-2s;26N;6-10s;17N |

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
题目内容
图表示一个质量为2kg的重物在竖直悬线的拉力作用下沿竖直方向向上运动的速度-时间图象。从图象可知,在________时间内,悬线的拉力最大,为________N;在________时间内,悬线的拉力最小,为________N。(g取10m/s2)

|
0-2s;26N;6-10s;17N |

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案